Greg's Response:

A vessel is defined here as storage, recycle, blend, or surge volume where there is no heat of reaction and no agitator. Fortunately, most vessel volumes are so large that the process time constant is extremely large and, consequently, the rate of change of temperature is exceptionally slow. This is fortunate because the only mixing typically provided in storage and feed tanks is provided by incoming flows (e.g., feed and recirculation) and convective currents. The addition of eductors and the location of dip tubes or spargers can greatly reduce the loop dead time magnitude. Ideally, thermowells should be installed in the elbows of recirculation lines. If they must be installed in the vessel, they should be in areas where the fluid velocity is largest, to reduce the measurement time constant, but farthest away from steam spargers, to avoid erratic nonrepresentative temperature readings. Storage and feed tank temperature loops often have a process time constant so large that a high controller gain can be used despite a high process dead time from poor mixing.

For throttling of coolant flow to coils or jackets of small vessels with a continuous discharge flow, the same concerns described for heat exchangers about a limit cycle from excessive dead time and process gain at low flow exist. Therefore, gain scheduling or signal characterization are useful techniques. Also, a feedforward signal can be computed, based on a simple energy balance as was done for the heat exchanger. A better solution is to keep a high constant coil or jacket recirculation flow and use a coil or jacket inlet secondary temperature control manipulate a makeup coolant flow to inlet with pressure control manipulation of return flow from coil or jacket outlet. When heating is required, steam flow to a steam injector in a high flow coil or jacket recirculation line manipulated by inlet temperature control provides the best dynamics. For vessel zero discharge flow, set point profiles and proportional-plus-derivative (PD) controllers (like those used on batch reactors) can help prevent overshoot.

Simulations that include operating conditions and equipment design with Digital Twin can help find and confirm the best control strategies.

For much more knowledge, see the ISA book Advanced Temperature Measurement and Control, Second Edition (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

Ron's Response:

Pattern recognition and tacit knowledge—the instincts gained through experience—are indispensable for problem-solving. But how do you cultivate these skills in a controlled environment? Simulation training provides the perfect solution:

• Dynamic Mental Networks: Simulators allow operators to build mental representations of how systems behave under various conditions. By repeatedly engaging with these systems, operators develop an intuitive understanding of how to anticipate and respond to changes. They also learn to validate that their responses were effective or need adjusting. 
• Recognizing Anomalies: The ability to spot subtle deviations is critical in preventing issues before they escalate. Simulation training sharpens this skill by exposing operators to diverse scenarios, helping them notice and interpret early warning signs.
• Applying Action Scripts: Experience breeds efficiency. Simulators enable operators to test and refine action scripts—quick, informed responses based on past experiences. This creates a toolkit of proven strategies for handling real-world challenges. Practicing emergency procedures on a simulator trains operations to quickly execute critical steps without hesitation. 

In a recent upset an experienced operator assisted at the console and quickly gathered the plant status. Determining that a PSV was about to lift and the current reduction in rates was not sufficient, he asked that the rates be reduced by one third using an application. This intervention likely prevented several days of lost production. 

Simulation training accelerates the accumulation of tacit knowledge. It gives operators the chance to repeatedly encounter and resolve complex problems, embedding lessons that would otherwise take years of real-world experience to learn. This training transforms knowledge into instinct, enabling operators to act quickly and decisively when it matters most.

In the posts that follow, we’ll dive deeper into the remaining perspectives, illustrating how simulation training transforms how operators approach challenges. Together, these elements foster growth, build expertise, and enable resilience in even the most dynamic and high-pressure situations. Let’s explore how simulation training goes beyond technical skills to shape a mindset that’s ready for anything.

Greg's Response:

Flows much lower than design causes a high process gain and high process deadtime that can lead to temperature oscillations and possible instability. Low velocities can cause a dramatic increase in fouling of heat transfer surfaces. Flows much higher than design causes a low process gain (poor sensitivity) that can lead to wandering of the temperature and possible loss of temperature control.

When peak error or initial transient must be minimized, feedforward control should be used. A rather simple energy balance that equates heat lost from the hot side to heat gain by the cold side yields a solution. Normal operating values are used for those inputs not measured that are relatively constant. For example, if the main upset is feed flow, a measurement of this flow is required, but assumed operating conditions can be used for the inlet temperatures that are not measured. It is critical that the controlled temperature be the set point rather than the measurement to avoid positive feedback. The feedforward signal is added to the output of the feedback controller. A bias of 50% is also subtracted so that the temperature controller can make a negative correction as large as the positive correction to the feedforward signal. The manipulated flow is best achieved by means of a flow controller and a cascade of exchanger temperature to coolant or steam flow. If the temperature controller output goes directly to a control valve, signal characterization of the installed valve characteristic should be used to convert from desired flow to required valve position. The signal divider for compensation of process gain nonlinearities should be applied to the controller output before the summer.

If the exchanger outlet temperature can be adjusted, a valve position controller can be used to slowly change the temperature set point to optimize the coolant valve position that minimizes the fouling of heat transfer surfaces by prevention of low throttle positions but also maintains the process gain and reduces utility usage by the prevention of high throttle positions.

Simulations that include operating conditions and equipment design with Digital Twin can help find and confirm the best control strategies.

For much more knowledge, see the ISA book Advanced Temperature Measurement and Control, Second Edition (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

Russ' Response:

Traditionally, process design uses steady state (SS) simulation, and it serves its purpose well.  Most analysis of processes and textbook instruction on how processes work use SS relations.  These could be termed static models, which represent process interactions, gains, and sensitivities when the process has lined out to steady operations.  

The problem is that SS models do not indicate how the process moves from an initial to a final SS.  The path it takes to move from one SS to another is termed a transient, which is described by dynamic models.  Dynamic models might be called time dependent, transient, or temporal models.  Understanding the transient can be essential.    

For instance:

• In a long pipeline, a rapid change in a flow control valve position or in switching a pump on and off can create a large temporary pressure excursion as the fluid accelerates or decelerates causing a water hammer or temporary cavitation effect.
• Changing flow rates can substantially change the transport delay in a delivery system, which may cause operators or controllers to overreact.  At SS it does not matter how long the line is, but a long line can cause a confounding delay that would not be revealed by SS simulation. 
• Changing tank levels can substantially change the lag-time in mixing.  This could greatly amplify over and undershoot pH response when there is a delivery line after the reagent valve that continues to drip after shutoff, or needs to be filled after the valve response.  SS analysis will not reveal this.  
• There are continual perturbations in composition, temperatures, and flow rates of inflows to a distillation column.  These may push the column into weeping or flooding situations, even though SS models using nominal conditions indicate that operation is permissible. 
• A short duration of an input perturbation to a process might washout from in-process dilution and have no impact, but a longer or larger might cause a specification or operational violation.  

• In designing a control system, one might find a clever solution using SS responses, which may not work in practice due to the process transient responses.  As much pride we might have in a technical solution, it is not the solution or the affirmation of our ability that is important.  Use dynamic simulation to quantify the bottom-line benefit to the organization.  

   

There are many benefits for using dynamic simulations to understand and test control-related functions and applications, including:

• Training operators and engineers to understand and manage the process.
• Teaching students about the fundamentals.
• Evaluating and demonstrating the economic benefit of the next level of advanced regulatory control or of model predictive control.  
• Safely testing automation algorithms such as for steady-state detection, fault detection, auto tuning, getting controller models, tuning algorithms, etc. 
• Safely testing process and control system design options for insensitivity to disturbances.
• Comparing control strategies for economic benefit (quality giveaway, constraint violations, waste generation, calibration error robustness, capital cost of devices, maintenance).  
• Generating data to test Big Data algorithms for developing models.

I encourage you to use phenomenological models in dynamic simulators that legitimately represent your process, as opposed to FOPDT, or trivial mechanistic, or empirical black-box models.  

In subsequent ProseraPods, I’ll introduce how to create your own first-principles models, how to simulate environmental vagaries, how to calibrate and validate models, and how to use the models to evaluate the various economic indicators of transient events.  I hope to visit with you later.  Meanwhile, visit my web site https://www.r3eda.com/ to access information about modeling, control, optimization, and statistical analysis.

Ron's Response:

Curiosity is the cornerstone of a problem-solving mindset. It’s about asking “why” at every opportunity—not just when something goes wrong but to understand the deeper principles at play. Simulation training nurtures this curiosity in several ways::

1. Knowledge Exploration: Operators are encouraged to go beyond procedural steps, digging into the "how" and "why" of process theory. Simulators provide a platform to test these theories in real time, offering insights into dynamic system behaviors.
2. Questioning Assumptions: After each scenario, operators can analyze their choices, reframe their mental models, and test alternative solutions. This reflective practice helps uncover blind spots and fosters adaptive thinking.
   Think back to the last time you struggled with a problem. Somewhere you made an assumption, either an incomplete mental model of the process or a piece of critical information was missed. 
3. Challenging Beliefs: Simulation training creates a safe space to challenge established practices. Operators can experiment with unconventional approaches and learn from unexpected outcomes, fostering innovation.

By cultivating curiosity, simulation training doesn’t just teach operators how to react—it inspires them to think critically, question norms, and seek better ways of doing things. The result? A growth mindset that empowers continuous learning and improvement.

In the posts that follow, we’ll dive deeper into the remaining perspectives, illustrating how simulation training transforms how operators approach challenges. Together, these elements foster growth, build expertise, and enable resilience in even the most dynamic and high-pressure situations. Let’s explore how simulation training goes beyond technical skills to shape a mindset that’s ready for anything.

Ron's Response:

To answer this question let us approach this from three different perspectives. There are three powerful perspectives that form the foundation of this mindset:

1. Curiosity and Openness to Possibilities
2. Pattern Recognition and Tacit Knowledge
3. Focus and Stress Management

Simulation training provides a unique opportunity to develop these traits by creating a safe environment where operators can explore, make mistakes, and learn without real-world consequences. It offers the ability to pause, reflect, and try again—uncovering new insights each time.

By cultivating curiosity, pattern recognition, and stress management, simulation training equips operators with the tools they need to excel in complex environments.

In the posts that follow, we’ll dive deeper into each perspective, illustrating how simulation training transforms how operators approach challenges. Together, these elements foster growth, build expertise, and enable resilience in even the most dynamic and high-pressure situations. Let’s explore how simulation training goes beyond technical skills to shape a mindset that’s ready for anything.

Greg's Response:

Temperature RTD sensors should use 4 wires and TC sensors should use extension wires of same material as sensor with length as short as possible to minimize the effect of electromagnetic interference (EMI) and other interference on the low-level sensor signal. The temperature transmitter should be mounted as close to the process connection as possible, ideally on the thermowell.

To minimize conduction error (error from heat loss along the sensor sheath or thermowell wall from tip to flange or coupling), the immersion length should be at least 10 times the diameter of the thermowell or sensor sheath for a bare element.  For high velocity streams and bare element installations, it is important to do a fatigue analysis because the potential for failure from vibration increases with immersion length.

The process temperature will vary with process fluid location in a vessel or pipe due to imperfect mixing and wall effects. For highly viscous fluids such as polymers and melts flowing in pipes and extruders, the fluid temperature near the wall can be significantly different than at the centerline. Often the pipelines for specialty polymers are less than 4 inches in diameter, presenting a problem for getting sufficient immersion length and a centerline temperature measurement. The best way to get a representative centerline measurement is by inserting the thermowell in an elbow facing into the flow If the thermowell is facing away from the flow, swirling and separation from the elbow as can create a noisier and less representative measurement. An angled insertion in can increase the immersion length over a perpendicular insertion. A swaged or stepped thermowell can reduce the immersion length requirement by reducing the diameter near the tip. Thermowells with stepped stems also provide the maximum separation between the wake frequency (vortex shedding) and the natural frequency (oscillation rate determined by the properties of the thermowell itself).

Tight fitting spring loaded sheathed sensors should be used to eliminate any air gap between the sensor sheath and the inside wall and bottom of the thermowell that dramatically increases the response time.

Simulations that include response time and velocity and composition at thermowell tip can confirm the best installation. 

For much more knowledge, see the ISA book Advanced Temperature Measurement and Control, Second Edition (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

1. Ensure distance from the equipment outlet (e.g. heat exchanger exit) and sensor at least 25 pipe diameters for a single phase to promote mixing (recombination of streams).
2. Verify the transportation delay (distance/velocity or volume/flow) from the equipment outlet (e.g. heat exchanger exit) to the sensor is less than 4 seconds.
3. Ensure the distance from the desuperheater outlet to the sensor provides a residence time (distance/velocity) that is greater than 0.2 sec
4. Use a RTD for temperatures below 400 *C to improve threshold sensitivity, drift, and repeatability by more than a factor of ten compared to TC if vibration is not excessive.
5. For RTDs at temperatures above 400 *C, minimize length without increasing conduction error and maximize sheath diameter to reduce error from insulation deterioration.
6. Be extremely careful using RTDs at temperatures above 600 *C. A hermitically sealed and dehydrated sensor can help prevent increase in platinum resistance from oxygen and hydrogen dissociation but reliability and accuracy may still not be sufficient.
7. For TCs at temperatures above 600 *C, minimize decalibration error from changes in composition of TC by best choice of sheath and TC type.
8. For TCs at temperatures above 600 *C, ensure sheath material compatible with TC type.
9. For TCs above temperature limit of sheaths, use the ceramic material with best thermal conductivity and design to minimize measurement lag time.
10. For TCs above the temperature limit of sheaths with gaseous contaminants or reducing conditions, use possibly purged primary (outer) and secondary (inner) protection tubes to prevent contamination of TC element and still provide a reasonably fast response.
11. In furnaces and kilns ensure location and design minimizes radiation and velocity errors.
12. Use immersion length long enough to minimize heat conduction error (e.g., L/D > 5).
13. Use immersion length short enough to prevent vibration failure (e.g., L/D < 20).
14. Ensure velocity is fast enough to provide a fast response (e.g., > 0.5 fps) and is fast enough to prevent fouling for sticky fluids and solids (e.g., > 5 fps).
15. For pipes, locate the tip near the centerline.
16. For vessels, extend the tip sufficiently past the baffles (e.g. L/D > 5).
17. For columns, extend the tip sufficiently into tray or packing (e.g. L/D > 5).
18. For TC, use ungrounded junction to minimize noise.
19. To increase RTD reliability, use dual RTD elements except when vibration failure is more likely due to smaller gauge in which case use redundant separate thermowells. 
20. To increase TC reliability, use sensors with dual isolated ungrounded junctions.
21. For maximum reliability, greater intelligence as to sensor integrity and to minimize the effect of drift, use 3 separate thermowells with middle signal selection.
22. Document any temperature setpoint changes made by an operator for loops with TCs so that they can be diagnosed as to possibly originating from TC drift.
23. Realize the color codes of TC sensor lead and extension wires change with country ensuring drawings show correct codes and electricians are alerted to unusual codes.
24. Use spring loaded sheathed TC and RTD sensor that fits tightly in thermowell to minimize lag from air acting as insulator (e.g., annular clearance < 0.02 inch).
25. If an oil fill is used minimize thermowell lag, ensure tars or sludge at high temperature do not form in thermowell and tip is pointed down to keep oil fill in tip.
26. Use Class 1 element and extension wire to minimize TC measurement uncertainty.
27. Use Class A element and 4 lead wires to minimize RTD measurement uncertainty.
28. Use integral mounted temperature transmitters for accessible locations to eliminate extension wire and lead wire errors and reduce noise.
29. Use wireless integral mounted transmitters assembled and calibrated by measurement supplier to eliminate wiring errors and errors and provide portability for process control improvement and to reduce calibration, wiring installation and maintenance costs.
30. Use “sensor matching” and proper linearization tables in the transmitter for primary control loops and in Safety Instrumented Systems achieving accuracy better than 1 *C.
    

Greg's Response:

Temperature is often the most important of the common measurements because it is an indicator of process stream composition and product quality. Temperature measurements are also essential for equipment protection and performance monitoring.

In the process industry 99% or more of the temperature loops use thermocouples (TCs) or resistance temperature detectors (RTD). The RTD provides sensitivity (minimum detectable change in temperature), repeatability, and drift that are an order of magnitude better than the thermocouple (Table 1). Sensitivity and repeatability are 2 of the 3 most important components of accuracy. The other most important component, resolution, is set by the transmitter. Drift is important for controlling at the proper setpoint and extending the time between calibrations. Operators often adjust setpoints to account for the unknown drift. When the TC is calibrated or replaced, the modified set point no longer works. The RTD is also more linear and much less susceptible to electro-magnetic interference.  The supposed issue of a slightly slower sensor response will be addressed in the next post on how to get the best installation.

Thermistors have seen only limited use in the process industry despite their extreme sensitivity and fast (millisecond) response, primarily because of their lack of chemical and electrical stability. Thermistors are also highly nonlinear but this may be addressed by smart instrumentation.

Optical pyrometers are used when contact with the process is not possible or extreme process conditions cause chemical attack, physical damage, or an excessive decalibration, dynamic, velocity, or radiation error of a TC or RTD.

Simulations that include sensitivity, repeatability, drift, and EMF noise can show the advantage offered by the RTD.

For much more knowledge, see the ISA book Advanced Temperature Measurement and Control, Second Edition (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

Ron's Response:

Let us first look at a definition from Kumar Dey “Centrifugal compressor surge is a characteristic behavior of the compressor that occurs in situations when inlet flow is reduced, and the compressor head developed is so low that it cannot overcome the pressure at the compressor discharge. During a centrifugal compressor surge situation, the compressor outlet pressure (and energy) reduces dramatically which causes a flow reversal within the compressor”. This is considered to be a very dangerous and detrimental phenomenon as it results in compressor vibration that results in the failure of the compressor parts.

Surge conditions have caused loss of efficiency, mechanical damage, loss of containment and loss of life. A compressor is most susceptible to surge during startup, reduced load or sudden load changes. Surge controllers can be managed by basic PID flow controllers or a dedicated controller system. 

Simulators have been successfully used to test and tune dedicated controller systems before they are installed in the process. This can reduce their commissioning time and allow the unit to return to full production sooner. It will also help to validate the accuracy of the control philosophy and expedite updating the startup procedures. 
Training panel operators to respond to surge conditions is also critical. Basic PID flow controllers are typically inadequate to handle large surge events and require operator intervention. This requires a large output increase on the controller that operators need to train for and be comfortable with. 

Dedicated surge controllers can handle surge events more effectively. Operators will need to be trained on its functionality and how to manage instrumentation failures. There are several flow, pressure and temperature transmitters that input to the controller that can drift or fail that can impact the control system. These failures can be practiced on a simulator to train the panel operators to detect failures and respond correctly to mitigate the impact. 

Simulators are an excellent tool to train operators regardless of the control system. They can also be used to test new systems to increase effectiveness and reduce commissioning time. During some upsets a panel operator may not have five minutes to choose a course of action, never mind six months. 

Fortunately, we have simulators to train our operators, and they do have a pause button so they can develop the skills required to pick up on cues, anticipate developments and validate their actions. Simulator training is not only about learning to complete tasks and execute procedures, but also about developing a thought process that is critical to responding to problems that have never been thought of. 

The Dynamic Mental Networks concept is an attempt to further our understanding of how process operators must navigate difficult problems in a dynamic environment. 

Greg's Response:

Lime feeders have a transportation delay that is proportional to the length of the feeder divided by its speed. This transportation delay may be several minutes. To eliminate the need to increase the vessel size and the agitation power, the lime rotary valve speed can be base loaded, and the pH controller can manipulate the conveyor speed or the influent flow. If the pH controller manipulates the waste flow, the dissolution time associated with an increased lime delivery rate is also eliminated. The level controller on the influent tank slowly corrects the lime rotary valve base speed if the waste inventory gets too high or low.

The dissolution time of pulverized dry lime can be greatly reduced by slaking the lime and making it into a slurry. For example, the dissolution time for pulverized dry lime of about 32 min, can be reduced as lime slurry to about 8 min. The dissolution time of lime slurry increases with age due to the agglomeration of small particles into larger particles, even though the lime slurry storage tank is mildly agitated. If the pH controller manipulates the lime feeder or water addition to the lime slurry storage tank, the equipment time constant of the slurry tank has the same effect as a slow valve time constant. To prevent adding this time constant to the loop, the lime feeder speed should be manipulated by a slurry tank level controller and the water addition rate ratioed to the lime feeder speed. The pH controller should manipulate the diluted lime slurry discharge flow that feeds the neutralization vessel. The diluted lime slurry discharge flow must be kept flowing by using a recycle loop to prevent settling and plugging in the reagent lines. A throttled globe valve will plug. The liner of a pinch diaphragm valve will fail due to erosion. Pulse width modulation of an on-off ball valve is the best alternative because it has the fewest maintenance problems and is relatively inexpensive to replace periodically.

Dynamic simulations with automation, equipment, and process dynamics including dissolution time are needed to determine the best lime system design.

For much more knowledge, see the ISA book Advanced pH Measurement and Control Fourth Edition (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

The time for solids to dissolve can be horrendous (minutes). Although the time for bubbles to dissolve is faster (seconds), the noise from fluctuations in concentration, besides the delay to complete dissolution, is problematic. For these reasons, using lime and ammonia for pH control is undesirable. Additional problems stem from highly viscous reagents, such as 97% sulfuric acid, that result in laminar flow in control valves and greater difficulty in mixing with process streams. Highly concentrated reagents cause extremely large reagent delivery delays due to low reagent flows (e.g., <1 gal/h). Strong acids and strong bases cause this same problem, and the additional difficulty of a steeper titration curve and the consequential need for more precise final control elements and possibly more neutralization stages. The following best practices are offered to provide more realizable reagents for pH control.

1. Avoid reagents that have solids or bubbles, take more than a second to react, are highly concentrated, or are strong acids or strong bases.
2. Increase the residence time in equipment and piping to provide complete dissolution of reagents and uniformity of reagents in the process stream.
3. If a conveyor is used, manipulate the motor speed of a gravimetric feeder rather than the flow dumped on the conveyor inlet to eliminate the conveyor transportation delay.
4. Use pressurized reagent pipelines with a coordinated isolation valve close coupled to the reagent control valve outlet to prevent process backflow into the reagent pipeline.
5. Minimize the volume between the reagent valve and its injection point into the process.
6. Avoid using dip tubes by injecting reagent into the feed or recirculation stream. 
7. Dilute reagents using tight concentration control in a recirculation stream to a diluted reagent storage tank.
8. Use Coriolis mass flow meters for accurate reagent flow and concentration measurement by using a high-resolution density measurement for reagent dilution and pH flow ratio control.
   

Ron's Response:

Whenever an incident occurs the investigators freeze time and slowly break down the sequence of events—viewing it from all perspectives. If only we could give our process operators this amount of time and reflection of the problems they encounter. David Woods, Resilience Engineer, discusses on a NDM podcast how the operators at Three Mile Island had 10 minutes to figure out something they were never told that could happen. Then after 6 Months and $60 million, the experts determined exactly what should have been done.

Operators must be able to make decisions and then respond to what happens. They must hedge their choices and be open to revision. There is always uncertainty whether the right choice has been made in our complex dynamic processes, where one action could impact several other systems.

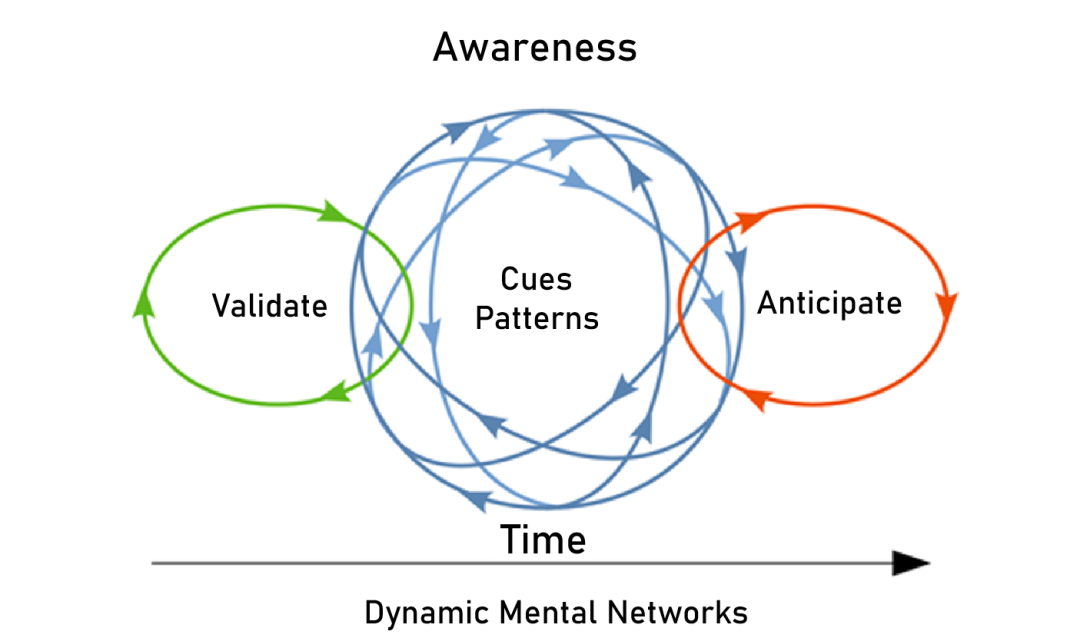
To graphically imagine what this might look like; I created the Dynamic Mental Network concept. We have previously discussed how picking up cues and pattern recognition can speed up problem detection and provide responses. The next challenge is to implement this in a complex, dynamic environment. When we have a complex mental model of the process, we can anticipate problems before they escalate, and we will also be able to anticipate the impact a problem will have on other systems to mitigate their effects.

Our panel operators must validate they have made the right choice while the process is in transition. Picking up on cues and patterns is a constant process to detect problems, anticipate what may be evolving, and validating that the solutions are effective. There is no pause button. During some upsets a panel operator may not have five minutes to choose a course of action, never mind six months.

Fortunately, we have simulators to train our operators, and they do have a pause button so they can develop the skills required to pick up on cues, anticipate developments and validate their actions. Simulator training is not only about learning to complete tasks and execute procedures, but also about developing a thought process that is critical to responding to problems that have never been thought of.

The Dynamic Mental Networks concept is an attempt to further our understanding of how process operators must navigate difficult problems in a dynamic environment.

Greg's Response:

A common misconception is that the slope of the titration curve and, therefore, the system sensitivity can be decreased by reagent dilution. Reagent dilution has a negligible effect on the shape of the titration curve: the curve slope will appear larger if the same abscissa is used because only a portion of the original curve is displayed. The numbers along the abscissa must be multiplied by the ratio of the old to the new reagent concentration to show the entire original titration curve. For example, the abscissa values would have to be doubled if the reagent concentration were cut in half. 

Properly designed dilution systems offer a variety of performance benefits. Most chemists use diluted reagents to make titration easier and more accurate. Because this is true for the lab, you can imagine how much more important it is in the field fraught with nonideal conditions. Dilution can reduce reagent valve plugging, reagent transportation delay, and reagent viscosity. It can prevent laminar flow and partially filled pipes and dramatically improve dispersion in a mixture. It also decreases the freezing point and winterization problem and corrosion for sodium hydroxide and plugging tendency. However, sulfuric acid becomes more corrosive when diluted. 

If reagent dilution is used, the system must be carefully designed to prevent creating reagent concentration upsets and delivery delays. The pH controller should throttle the diluted reagent. The mass flow of water should be ratioed to the mass flow of reagent, and a density controller should trim the ratio. Coriolis flow meters should be used to improve the mass flow measurement reproducibility and provide an accurate density measurement for concentration control. In addition, one could utilize the temperature from the Coriolis meter to compensate for the density, particularly if the feed temperature is not constant. For steep titration curves and in-line pH control, a storage tank for a diluted reagent with a high recirculation flow should be installed to smooth out the fast reagent concentration disturbances from the dilution.

Dynamic simulations with piping and control system dynamics are needed to determine the best liquid reagent dilution design.

For much more knowledge, see the ISA book Advanced pH Measurement and Control Fourth Edition (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

Greg's Response:

If the reagent pipeline is partially filled or empty or a dip tube is backfilled with process fluid, the regent delivery delay becomes the biggest source of dead time in a pH loop for the small reagent flows commonly required for neutralization. Whenever a reagent control valve closes or a metering pump stops, the reagent continues to drain into the process, and process fluid can be forced back up into the reagent injection or dip tube. Even if hydraulics do not promote much drainage or backfilling of the dip tubes, ion migration from high to low concentrations will proceed until an equilibrium is reached between the concentrations in the reagent tube and the process volume. As a result, the pH will continue to be driven by the drainage and migration of reagent after the control valve closes or the metering pump stops. If the valve is closed or the pump is stopped for a long time, when the valve opens or the pump starts, it must flush out process components in the tubes before the reagent gets into the volume. The worst-case delivery time delay is the volume of the backfilled tube divided by the reagent flow. Because dip tubes are designed to be large enough to withstand agitation and the design standard for normal flows is to take the dip tube down toward the impeller, the reagent delivery delay can be several orders of magnitude larger than the turnover time.

If reagent piping is totally filled with a constant concentration of noncompressible liquid reagent, a change in valve position initiates a change in reagent flow within a second or two. An automated on-off isolation valve close-coupled to the process connection that closes when the control valve throttle position is below a reasonable minimum helps keep reagent lines pressurized and full of reagent. Injection of reagent into recirculation lines with a high flow rate just before entry into the vessel instead of via dip tubes offers a tremendous decrease in reagent delivery delay.

Dynamic simulations with piping and dip tube dynamics are needed to determine the best liquid reagent delivery design.

For much more knowledge, see the ISA book Advanced pH Measurement and Control Fourth Edition (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

Greg's Response:

For a reagent dose to be precise enough, the reagent’s logarithmic acid dissociation constant (pKa) should be close to the pH set point so that it tends to flatten the titration curve. The reagent viscosity should be low enough to ensure a fully turbulent flow which is important for consistent dosing. The reagent should be free from solids and slime because of the tiny control valve trims used. A fast reagent delivery requires that the reagent viscosity be low enough for the dose to start quickly and mix rapidly with the effluent. An extraordinary time delay has been observed for starting the flow of 98% sulfuric acid through an injection orifice because of its high viscosity. It has been compared to getting ketchup out of a bottle. Mixing an influent stream with a viscous reagent stream, such as 98% sulfuric acid or 50% sodium hydroxide that is about 40 times more viscous than the typical influent stream, is difficult and requires greater agitation intensity and velocity. A highly viscous reagent dose tends to travel as a glob through the mixture. Lastly, the reagent should be in the liquid phase.

The neutralization reaction of liquid components is essentially instantaneous once reagent streams are mixed with influent streams. Gas or solid reagents take seconds and minutes, respectively, to dissolve and get to actual liquid contact and mixing with the influent stream components. Reagent bubbles escape as a vapor flow when the bubble breakup time and gas dissolution time exceed the bubble rise time. Coating and plugging upstream control valves and downstream equipment from particles of unreacted reagent or precipitation of salts from reacted reagents can be so severe as to cause excessive equipment maintenance and downtime. Liquid reagents such as ammonia can choke the control valve from flashing in vena contracta or cause cavitation damage in the valve and the piping immediately downstream. Particles in the reagent can erode the valve trim. Some waste lime systems have rocks that can quickly tear up a valve seat and plug.

Dynamic simulations with representative physical properties and phases are needed to determine the best reagent.

For much more knowledge, see the ISA book Advanced pH Measurement and Control Fourth Edition (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

Ron's Response:

In the last pod we discussed how stress can impact performance and what are some of the physiological responses to stress. 

In her book, The Unthinkable: Who Survives When Disaster Strikes, Amanda Ripley discusses the three stages people go through when responding to critical situations. The first can be Denial when we may try to normalize the event and try to fit the event into past patterns and experiences. The next is Deliberation when we like to form groups to discuss what is happening and get support. The last is the Decisive moment when we take action to respond to an event.

To get past the Denial step we can highlight the key parameters or indicators that a particular event has happened. For example, if a primary compressor trips and requires the facility to go to a safe park state, what emergency alarms will come in? Is there a speed indicator that can be referred to?  Knowing the key indicators will help move the panel operator through denial quickly. 

Deliberation can happen before an event during training. Discuss why the responses from a procedure are important and what impact they will have on the process. This discussion should happen before the response is practiced on the simulator.  Sharing similar events or stories can also help to move through the Deliberation step faster. 

Training and experience can help us move to the Decisive step faster and lessen the impact of an event. Simulator training is an excellent tool to minimize the effects of stress during critical incidents. Emergency procedures can be practiced which will allow an operator to put together the responses required to all the systems and how they can impact each other.  A procedure is written in a linear fashion, the actual process is much more dynamic with many interacting systems. 

A loss of containment and how to provide isolation can also be practiced on a simulator. This will lessen the stress responses if a similar event occurs and prepare operations to make key decisions for these events. 

Even though an incident may not evolve the same way every time, training will develop pattern recognition skills that will help to minimize stress and the physiological responses.  

Greg's Response:

Stick and slip generally occur together and have a common cause of friction in the actuator design, stem packing, and seating surfaces. Rotary valves with high temperature packing and tight shutoff (the so-called high-performance valve) exhibit the most stick-slip. Rotary valves tend to also have shaft windup where actuator shaft moves but the ball, disc, or plug does not move. It is much worse at positions less than 20% where the ball, disc, or plug is starting to rotate into the sealing surfaces. For sliding stem (globe) valves, the stick-slip increases below 10% travel as the plug starts to move into the seating ring. These problems are more deceptive and problematic in rotary valves because the smart positioner is measuring actuator shaft position and not the ball, disc, or plug stem. If there is stick-slip, the controller will never get to the set point and there will always be a limit cycle. The biggest culprits are low leakage classes and the big squeeze from graphite and environmental packing particularly when they are tightened without a torque wrench. A bigger actuator may help but does not eliminate the problem.

For the best throttling valves (globe valves with diaphragm actuators), the stick-slip is normally only about 0.1% and its effect is typically observable only in pH system trend recordings.  The control valve resolution will clearly show up as a large sustained oscillation for a set point on the steep portion of the titration curve because of the high process gain. The extreme sensitivity of the pH process requires a valve resolution that goes well beyond the norm. The number of stages of equipment needed for neutralization may be dependent on the capability of the control valve. It is difficult to effectively use more than one control valve per stage. An extremely small and precise control valve is necessary to keep limit cycle within the control band. To achieve the large range of reagent addition and extreme precision required, several stages are used with the largest control valve on the first stage and the smallest control valve on the last stage.

Dynamic simulations with control valve resolution and lost motion included are needed to determine the best control valve and number of neutralization stages.

For much more knowledge, see the ISA book Advanced pH Measurement and Control Fourth Edition (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

The achievement of a fast and precise final control element is critical for pH control. The focus on control valve resolution and rangeability is an essential starting point but there are many other considerations. Also, variable frequency drives (VFDs) are often touted as offering tighter control but there are many design and installation choices made that can make this expectation unrealistic. To help us all to be aware of potential problems and recognized solutions, the following list of best practices is offered based on the content in Chapter 7 of the ISA book Essentials of Modern Measurements and Final Elements in the Process Industry.

1. Use sizing software with physical properties for worst case operating conditions.
2. Include effect of piping reducer factor on effective flow coefficient.
3. Select valve location and type to eliminate or reduce damage from flashing.
4. Preferably use a sliding stem valve (size permitting) to minimize backlash and stiction unless crevices and trim causes concerns about erosion, plugging, sanitation, or accumulation of solids particularly monomers that could polymerize and for single port valves install “flow to open” to eliminate bathtub stopper swirling effect.
5. If a rotary valve is used, select diaphragm actuator with splined actuator shaft to stem connection, integral cast ball or disk stem, and minimal seal and packing friction to minimize lost motion deadband and resolution limitation.
6. Use conventional Teflon packing, and for higher temperature ranges use Ultra Low Friction (ULF) Teflon packing, avoid overtightening of packing, and consider possible use of compatible stem lubricant. 
7. Compute the installed valve flow characteristic for worst case operating conditions.
8. Size actuator to deliver more than 150% of the maximum torque or thrust required.
9. Select actuator and positioner with threshold sensitivities of 0.1% or better.
10. Ensure total valve assembly deadband is less than 0.4% over the entire throttle range.
11. Ensure total valve assembly resolution is better than 0.2% over the entire throttle range.
12. Choose inherent flow characteristic and valve to system pressure drop ratio that does not change the valve gain more than 4:1 over entire process operating point range and flow range. 
13. Tune the positioner aggressively (high proportional action gain) for application without integral action with readback that indicates actual plug, disk or ball travel instead of just actuator shaft movement.
14. Never replace positioners with volume boosters. Instead put volume boosters on the positioner output to reduce valve 86% response time for large signal changes with booster bypass valve opened just enough to assure stability.
15. Use small (0.2%) as well as large step changes (20%) to test valve 86% response time to see if changes need to be made to meet desired 86% response time.
16. See ISA TR75.25.02 Annex A for more details on valve response and relaxing expectations on travel gain and 86% response time for small and large signal changes, respectively. 
17. Counterintuitively increase the PID gain to reduce oscillation period and/or amplitude from lost motion, stick-slip, and from poor actuator or positioner sensitivity. 
18. Use external-reset feedback detailed in Chapter 8 with accurate and fast valve position readback to stop oscillations from poor precision and slow response time.
19. Use input and output chokes and isolation transformers to prevent EMI from the VFD inverter.
20. Use PWM to reduce torque pulsation (cogging) at VFD low speeds.
21. Use a VFD inverter duty motor with class F insulation and 1.15 service factor, and totally enclosed fan cooled (TEFC) motor with a constant speed fan or booster fan or totally enclosed water cooled (TEWC) motor in high temperature applications to prevent overheating.
22. Use a NEMA Design B motor instead of Design A motor to prevent a steep VFD torque curve.
23. Use bearing insulation or path to ground to reduce bearing damage from electronic discharge machining (EDM). Damage from EDM is worse for the 6-step voltage older VFD technology.
24. Size the pump to prevent it from operating on the flat part of the VFD pump curve.
25. Use a recycle valve to keep the VFD pump discharge pressure well above static head at low flow and a low-speed limit to prevent reverse flow for highest destination pressure. 
26. Use at least 12-bit signal input cards to improve the VFD resolution limit to 0.05% or better
27. Use drive and motor with a generous amount of torque for the application so that speed rate-of-change limits in the VFD setup do not prevent changes in speed from being fast enough to compensate for the fastest possible disturbance.
28. Minimize VFD deadband introduced into the drive configuration (often set in misguided attempt to reduce response to noise) causing delay and limit cycling. 
29. For VFD tachometer control, use magnetic or optical pickup with enough pulses per shaft revolution to meet the speed resolution requirement.
30. For tachometer control, keep the speed control in the VFD to prevent cascade rule violation where the secondary speed loop is not 5 times faster than the primary process loop. 
31. To increase rangeability to 80:1, use fast cascade control of speed to torque in the VFD to provide closed loop slip control.
32. Use external- reset feedback with accurate and fast speed readback to stop oscillations from poor VFD resolution and excessive deadband and rate limiting in VFD configuration.
33. Use foil braided shield and armored cable for VFD output spaced at least one foot from signal wires never any crossing of signal wires, ideally via separate cable trays.
    

Ron's Response:

Capt. Chesley “Sully” Sullenberger was quoted as saying that the moments before the emergency water landing of US Airways Flight 1549 were "the worst sickening, pit-of-your-stomach, falling-through-the-floor feeling" that he had ever experienced. This was after a forced landing in the Hudson River because a bird strike shutdown both engines. I can relate to this feeling.

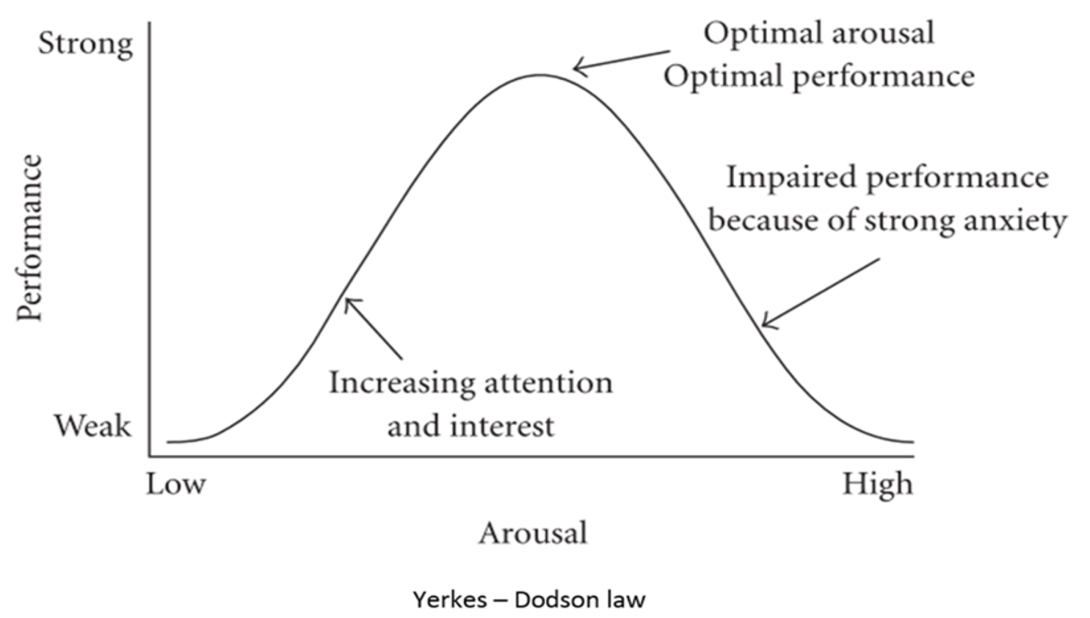
Referring to the above diagram we can see that not all stress is bad. We need some arousal to keep us interested. However, if the stress is too high it can impair our performance. What your peak performance is, can depend on your experience and training. 

There can be physiological responses to high stress situations. The brain may revert to a primitive response which overrides higher functions. Time may seem to slow down or speed up. Tunnel vision may limit the ability to see the big picture. Tunnel hearing may occur or a loss of hearing. A feeling of detachment may be experienced or feelings of dissociation. Coordination may be affected or shaking hands my impair the use of a keyboard. Speech may be affected, either a loss or a shrill voice that may be hard to understand. Most People do not normally panic. They are more likely to freeze and minimize the severity of the event.

In the next pod we will discuss how we respond to critical situations and how we can train and prepare for them.   

Greg's Response:

Static mixer have noisy pH measurements. Signal filtering can help but a downstream volume is needed to provide smoothing of pH oscillations that can be larger than 6 pH for steep titration curves.

Static mixers have motionless internal elements that subdivide and recombine the flow stream repeatedly and cause rotational circulation to provide radial mixing of the stream but very little axial or back mixing. Consequently, fluctuations in pH over the cross section are smoothed, but fluctuations in pH with time, which are axial, show up unattenuated in the discharge. The equipment dead time is about 80% of the residence time for a static mixer, and most manufacturers are working toward making their static mixers exhibit plug flow to reduce the residence time distribution. Although this is beneficial for many chemical reactions, it makes the discharge pH more likely to oscillate, spike, and violate constraints.

Flow pulses from a positive displacement reagent pump and drops associated with a high-viscosity reagent or low reagent velocity will not be back mixed and will cause a noisy pH signal. Bubbles from a gaseous reagent will also cause a noisy pH signal because the residence time is not sufficient for complete reagent dissolution. Although a static mixer has a poor dead-time-to-time-constant ratio that tends to make a pH loop oscillate, it offers the significant advantage of a small magnitude of dead time and a small volume of off-spec material from a load upset. Also, the reagent injection delay for close coupled reagent valves is much less than for vessels.

The fast correction and small dead time mean that a static mixer used in conjunction with a volume can eliminate the need for a well-mixed vessel. The static mixer can be on the feed or recirculation line of a volume. pH waste treatment systems use static mixers in series separated by volumes. The volumes may simply use an eductor to provide some mixing for smoothing of the oscillations.

Dynamic simulations with mixing nonuniformity and dead time can show the best use of static mixers in conjunction with vessels.

For much more knowledge, see the ISA book Advanced pH Measurement and Control Fourth Edition (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

Equipment and the associated piping are the most frequent and largest sources of loop dead time. The lack of understanding of how mixing profiles and especially the fundamental concept of back mixing and the transportation delay of reagent into the mixture, and the transportation delay of changes in process pH appearing at the electrode are the biggest detriments to pH control system performance, assuming a healthy electrode and precise final control element.   To minimize these problems, the distances to and from the mixture are minimized, the axial agitator pumping rate in vessels for back-mixing is maximized, and dead zones are minimized. Strategically employing vessels and static mixers in various pH control system designs and the importance of minimizing dead time will be detailed in future posts on pH control system design.

1. In equipment where a pH control system injects reagent, minimize the dead time contribution to the loop dead time from mixing and transportation delays to less than 6 s.
2. Use large volumes susceptible to large dead times upstream or downstream of the pH control system to average out pH changes for smoother pH control and less reagent consumption, particularly by upstream volumes where influent pH swings above and below the pH set point.
3. If large volumes exist downstream for smoothing pH fluctuations, a static mixer with a close-coupled reagent injection to the mixer inlet and electrodes in the pipeline about 20 pipe diameters downstream of the mixer outlet is an option for fast pH control to minimize new equipment cost.
4. Use static mixers in the feed or recirculation line of the vessel to premix influent and reagent added to the static mixer inlet to minimize mixing and injection delays.
5. Use impellers designed for axial agitation in vessels where a pH control system injects reagent. Keep the vessel diameter-to-height ratio between 0.5 and 1.5 and the agitator pumping rate to give a turnover time (mixing dead time) significantly less than 6 s.
6. In vessels where a pH control system injects reagent, use baffles in the well-mixed vessels to prevent dead zones and promote an axial agitation flow pattern.
   

Ron's Response:

Developing a simulator program involves a financial commitment and resources to be successful. This continues after the initial installation of the facility. One of the first questions asked when considering a simulator facility is the cost and how it can be justified. It is a business decision like any other new improvement to the process. 

There are several ways to justify a simulator program. I believe the largest is operator competency. To be blunt, no one wants their company to be part of a Chemical Safety Board bulletin. This does not mean that it was operations that caused the incident, it means that if they must respond to an evolving situation and if they are more than just qualified, they may be able to prevent an incident from escalating. These types of incidents involve the loss of life, hundreds of millions of dollars of production losses, and equipment damages. It is difficult for someone who has not worked a control panel during an upset to imagine how quickly you can become cognitively overloaded. 

To maintain competency tasks must be practiced periodically. Reliability improvements and the time between major maintenance shutdowns being extended can leave operations rusty in executing these tasks. A simulator recertification program will ensure operations is prepared to respond to upsets and safely handle shutdowns. 

Simulator programs have become a key instrument in improving our environmental performance and reducing flaring. This is a natural extension of on-stream time. Shutdowns and startups require flaring. Strategies to reduce flaring can be trialed on a simulator. Several approaches can be tested and refined while measuring the amount of flaring required. Safe Park applications can be developed and tested with a simulator with flaring reductions in mind. 

Advanced control systems can be developed and tested on a simulator. There are always challenges implementing these systems that are difficult to anticipate in our dynamic processes. Flushing these out on a simulator reduces process upsets and flaring. The run time of these control systems can also be improved by training the operators on their function and how to troubleshoot problems. 

Control system software updates can be tested on a simulator. This not only highlights errors, but it also gives the control technicians a chance to train and perfect the software roll out. Major process upsets have occurred from control system software updates. Of course, the most effective testing is when the simulator system as close to the live system as possible. 

Periodically the control system is replaced with new hardware and software. This is a very disruptive period for operations as it typically involves new graphics and interfaces. These can be developed and tested on a simulator to minimize the errors in the diagrams and the links from the objects. Operations can also be trained on the new graphics to complete routine tasks and to manage upsets. New graphics can considerably slow down even an experienced operator until they learn where to find everything.

There are many ways to justify a simulator program. In many facilities if you can increase your onstream time by 1% the program will more than pay for itself. 

Greg's Response:

pH systems are extremely sensitive to the vessel design. A poor design can make good pH control impossible in nearly all systems despite the use of the most advanced control techniques.

In vessels, there are many different internal flow patterns from agitation and many different parameters to quantify the amount of agitation. For pH control, the flow pattern should be axial, where the fluid is pulled down from the top near the shaft, circulated along the bottom to the sidewalls, and pulled back up to the top near the sidewalls. If the agitation breaks the surface without froth, its intensity level is in the ballpark for good pH control. The pattern is called axial because of the vertical up-and-down flow pattern parallel to the axis of the shaft. Baffles that are 90 degrees apart, extend vertically along the entire length of the sidewall, and are one-sixtieth of the diameter in width are recommended because they help establish the vertical flow currents to reduce vertexing, swirling, and air induction from the surface, plus they increase the uniformity of the flow pattern. Propeller and pitched blade turbines provide an axial flow pattern. A double-spiral blade and a tangential jet nozzle cause an undesirable corkscrew axial pattern because the concentration change has a long and slow corkscrew flow path.

For a vessel with axial agitation, baffles, and a liquid height that is about the same as the diameter, the equipment dead time is approximately the turnover time that can be estimated as the liquid mass divided by the summation of the influent, reagent, and recirculation flows plus the agitator pumping rate. If the ratio of the equipment dead time to the time constant is equal to or less than 0.05, the vessel is classified as a vertical well-mixed tank. Horizontal tanks have a length much greater than the height. No matter how many agitators are installed, the complete volume cannot be considered as axially mixed. There will be regions of stagnation, short-circuiting, and plug flow.

Dynamic simulations with mixing nonuniformity and dead time can show the importance of a vertical well-mixed tank.

For much more knowledge, see the ISA book Advanced pH Measurement and Control Fourth Edition (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

Aaron's Response:

When we talk about ROI in a modernization, we are really talking about enabling the ROI of automation, given a modern DCS.  This requires a change in automation approach but can deliver big returns.

The primary value categories fall into the following:

1. Throughput
   • Bringing the process up to its level of expected performance
2. Safety
   • Utilizing automation to expose fewer people to the process
   • Automated handling of abnormal situations or infrequent situations
   • Reducing probability of incidents due to human error
3. Consistency
   • Optimal control strategies and operating/tuning parameters under any given condition
4. Digitalization
   • Asset optimization and insight through the DCS to plant personnel
   • A Path for data analytics to empower enhanced decisions.

Unfortunately, reaching these goals often requires a more modern DCS than what is installed. Beyond that, that DCS needs to be instrumented and automated beyond what is typically seen – especially in industries outside of perhaps life sciences and modern specialty chemical installations.

To deliver on the potential value here, simulation plays an important role. It mitigates risk by allowing for development, testing, and iteration on automation without process impact. This is key for driving production throughput and improved safety. And for those consistency applications, simulation can help with the development of state-based or dynamic control strategies as well as to train the operators through those varying operating conditions and state transitions.  The interface between the process and operations post-optimization may be very different than before. Done right, this improved automation can deliver major improvements.  

Some benchmarks we have seen include:

• 5% increased equipment capacity
• 5% Energy and utilities reduction
• .5% Yield improvements (savings through reduced feedstock)
• 20% Reduction in transition times between products/grades
• 20% Reduction in off-spec product
• 10% Reduction in abnormal events
• 5% Reduction in reduced undesired byproducts
• 20% Reduction in re-blending costs
• 10% Reduction in inventories
• 20% Reduction in unscheduled maintenance
• 1% Reduction in unscheduled downtime

Applied to a large process, these benefits can be massive – certainly worth the investment in automation, including dynamic process simulation.

Ron's Response:

Several years ago, Gary Klein and Joseph Borders completed a study of operators’ mental models that involved watching how they navigated through process upsets on a simulator (This was through the Center for Operator Performance).  From this, they developed the Mental Model Matrix. The matrix explores the relationship between the user and the system, as well as the capabilities and limitations of each system.

Operators must understand how the system was designed i.e. process theory and they must also understand how to make the system work in a dynamic environment. You may believe these are the same things, but they are not. Without going into too many details, I can think of several instances where operations have compensated for poor design or unintended consequences when the process is off-normal operating conditions or in a startup. It is important to design these quirks into a training simulator so the operators can be accustomed to them.

It is beneficial if operations understand how the equipment can fail. This will allow them to size up situations faster. There can be any number of problems with transmitters, valves, analyzers, pumps, or equipment fouling.  There is a belief that automation, digitalization, and artificial intelligence will solve many problems and generate more profits. They can do both, however, they also come with new challenges. They are only as reliable as the data (The Boeing 737 Max is one example worth noting). I believe that more training will be required for operations to be able to problem solve and troubleshoot these new tools. Simulators are the best way to accomplish this. Testing these tools on a simulator or digital twin before they are implemented will increase their success and minimize process upsets. 

The matrix also discusses how operators can become confused from the information they are receiving. Graphics design can make a large difference in minimizing this. This is a huge topic and deserves more research with the user’s input. At the very least a senior panel operator should be involved when the graphics are developed. The graphics should help develop the panel operator’s mental model and enhance their decision-making abilities. 

Knowing the capabilities and limitations of the process and the people is critical to maintaining production and safely managing our processes.

For more information visit the following:

Sage Journals The Mental Model Matrix 

Psychology Today The Mental Model Matrix

Greg's Response:

The titration curve is the most important piece of information for designing, commissioning, and troubleshooting pH control systems. Lab titration curves are typically done by placing a known volume of the process sample in a Pyrex glass jar and logging the pH indication for each incremental volume of reagent added via a burette. The volume of reagent added between the data points must be reduced drastically near the equivalence point. If the sample or reagent contains a strong acid or base, it is difficult to generate data points near the equivalence point.

If the titration curve has a long, flat tail, relatively few data points are needed until the first bend. However, the starting point representing the influent pH for various operating conditions must be plotted accurately to estimate the valve rangeability and stick-slip and the mixing equipment size and agitation requirements.

If the sample volume is given and the concentrations of the reagent used in the lab and the control system are equal, the reagent volumetric flow can be calculated for a given influent flow and pH. The titration curve used for system design should have an abscissa that is the ratio of reagent to influent flow.

The lab temperature during titration is rarely equal to the process temperature. The sample pH will change with the temperature because the dissociation constants change with the temperature. This is a change in actual solution pH and is not to be confused with the change in millivolts generated by the glass electrode per the Nernst equation. Conventional temperature compensators use a temperature sensor embedded inside the electrode to correct for the Nernst effect.

Every sample must be time-stamped with the exact time sample was taken. If the titration curve changes with time, separate samples should be gathered over a representative period and titrated individually. The samples should not be combined for titration.

Use a charge balance for a solution at the same temperature as the process with all the acids, bases, and salts including the change in dissociation constants with temperature and with carbonic acid added to match lab titration curves.

Dynamic simulation can significantly enhance the design of optimal titration curves for pH system management by addressing several key challenges. These include simulating high-resolution data near the equivalence point with adjustable reagent volumes, incorporating temperature-dependent dissociation constants to reflect process conditions, and modeling the effects of variable influent pH levels on system dynamics. The simulation can also account for the complexities of mixing, reagent concentration variations, and temporal changes in sample composition. Using simulation technology, combined with rigorous validation against experimental data, this approach promises to refine and optimize titration processes, ensuring more accurate and effective pH control systems.

For much more knowledge, see the ISA book Advanced pH Measurement and Control Fourth Edition (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

Top 20 Mistakes in Lab Titration Curves

1. An insufficient number of data points was generated near the equivalence point.
2. The starting pH (influent pH) data points were not plotted for all operating conditions.
3. The curve does not cover the whole operating range, including control system overshoot.
4. There is no separate curve zoom-in to show the curvature in the control region.
5. There is no separate curve for each different split-ranged reagent.
6. The effect of the sequence of the different split-ranged reagents was not analyzed. 
7. The effect of back mixing different split-ranged reagents was not considered.
8. The effect of overshoot and oscillation at the split-ranged point was not included.
9. The sample or reagent solids dissolution time effect on the abscissa was omitted. 
10. The gaseous reagent dissolution time and escape effect on the abscissa were omitted. 
11. The sample volume was not specified. 
12. The sample time was not specified.
13. The reagent concentration was not specified. 
14. The sample temperature during titration was different than the process temperature. 
15. The influent sample was contaminated by absorbing carbon dioxide from the air. 
16. The influent sample was contaminated by absorbing ions from the glass beaker.
17. The influent sample composition was altered by evaporation, reaction, or dissolution. 
18. The laboratory and field measurement electrodes had different types of glass. 
19. A composite sample was titrated instead of individual samples. 
20. The laboratory and field reagents used different compounds.

Aaron's Response:

Fundamentally, I think this is a two-way street. The way that simulation has changed the way I approach system modernization projects has shifted almost hand-in-hand with the way that modernization projects themselves have shifted.

For years, the only place dynamic simulation was really used was at the very end of the project, and, even then, in the most basic way possible. By providing simple I/O tiebacks, project teams could be sure that the basic scaling, control direction, and alarms were correct, and that the system graphics were configured properly and tied into the right points. With this very limited utility (which would be thrown away at the end of the project), the incentives were to spend as little time and effort as possible on the simulation.

Now that the utility of simulation throughout the project and operational lifecycle are more broadly understood, dynamic simulation becomes a living, growing risk mitigator/trainer/decision-maker. If they’re no longer throwing it away, then process manufacturers feel much more positive about investing in dynamic simulation. And with a heavier investment in dynamic simulation, they then look for more opportunities for it to deliver value.

Unfortunately, old habits die hard. Even though the project mindset and operational direction has somewhat evolved, the purchasing and procurement habits of the past have still lingered in many cases. If the project scope doesn’t explicitly require dynamic simulation, then automation vendors are likely to leave it out of the scope or to minimize its use. The project bidding process can be cutthroat, and vendors will look for opportunities to get their prices lower and win the project. It is critical that users who are considering modernizing their plants also consider the long-term benefits and the project risk reduction associated with dynamic simulation, and that they grow in the ways they put together bid packages and procurement-based vendor assessments.

Thankfully, the highest-performing organizations have already started to evolve in this way. They have evaluated vendors and negotiated master supply agreement (MSA) pricing ahead of time to clear the air of this type of “race to the bottom” approach. With pricing already secured, vendors and manufacturers can work hand in hand to do the right thing long-term for the facility – reducing risks in the right spots but not over-investing/”gold plating” a given project. This starts early in the project during the FEL-2/Select phase (even earlier than the FEED).

Then the use of simulation can be better specified in the FEED itself, including those particular areas where it provides the most near-term value (perhaps integration testing, operator training, etc). The simulation can appropriately grow over time. Perhaps most critically, knowing that this dynamic simulation capability is available which then frees up the engineering team to move away from that “replacement in kind” mindset that I mentioned and instead set their sites on legitimate control improvements that deliver real ROI (and now might be possible without added risk).

Ron's Response:

Unfortunately, far too many simulators have become dust collectors after their initial installation. They may have been developed for the initial startup of a facility and then forgotten about. There are several ways to prevent this from happening. 

The first is to have a dedicated trainer. They will be responsible for training the panel operators. This will include developing training scenarios and setting up a training schedule or a scheduling tool. A seasoned panel operator is the best fit for this position. The trainer will also be responsible for documenting problems that require maintenance and scheduling the appropriate people to complete the maintenance. 

Maintenance of the simulator is an important factor to ensure the training is relevant. The simulator requires the same update whenever there is an update in the facility.  One of the best ways to keep the simulator updated is when there is a project in the unit, the update to the simulator will be paid for by the project. This eliminates the need to justify another project to update the simulator. The control system specialists will also be required to install software updates and maintain the simulator hardware.  It takes a team to maintain a simulator.

I recommend having access to the simulator’s engineering interface to allow small fixes to the model and to enable small tuning of the simulator. This is an ongoing process and enables minor changes to be managed promptly. Some training from the simulator supplier will be required. Remember to always save a backup of the model before making changes. 

Leadership support is another crucial element for a simulator program. Leadership will approve the budget and make time available for the panel operators to attend their training. There are scheduling and financial aspects of this. It will take regular reminders of the benefits of the simulator program. Create a point form of the program benefits to share with executive leadership when they tour the facility. 

A simulator program requires support from several disciplines and a dedicated trainer who will be the champion of the program. 

Greg's Response:

Because of the pressure to minimize capital costs, a project may sell itself short on the number of stages required. The basic rule from the 1970s was that a well-mixed tank is needed for every two pH units that the influent feed pH is away from the set point. For example, if the set point was 7 pH, one stage for an influent at 5 pH, two stages for an influent at 3 pH, and three stages for an influent at 1 pH would be required. The modern-day version of this old rule would reduce the requirement by one stage if feedforward control or signal linearization could be used effectively or if the set point could be moved to a flatter portion of the titration curve. Today, three stages are rarely used. Even the most difficult systems are tackled by an inline system for the first stage, followed by a well-mixed vessel for the second stage.

One of the most frequently missed opportunities in dramatically reducing the difficulty of control and saving on reagent usage is to shift the set point away from the center to the edge of a control band where the slope is flatter. For example, many environmental systems must keep the effluent between RCRA 2 and 12 pH limits to avoid being classified as hazardous waste. However, a set point at 7 pH is the wrong choice and may lead to oscillations between 2 and 12 pH. A much better choice would be an optimized set point of 4 pH for acidic influent and 10 pH for basic influent.

While a tank with minimal agitation may suffice for blending and smoothing, a vessel with direct reagent addition for pH control must be well mixed with a residence time greater than 5 minutes for maximum process flow and at least 20 times the turnover time.

A dynamic simulation that uses a charge balance with all acids, bases, and salts, verified titration curve, process time constants, transportation, injection, and mixing delays, noise, and measurement and valve 5Rs is critical for finding the best and lowest cost pH system design. 

For much more knowledge, see the ISA book Advanced pH Measurement and Control Fourth Edition (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

Top 12 Mistakes Made Every Day in pH System Design

1. Incorrect or missing titration curve (incorrect process gain and sensitivity).
2. Improper vessel geometry and agitation patterns (excessive equipment dead time).
3. Backfilled reagent dip tube (excessive reagent injection delay).
4. Incorrect location of reagent injection point (short-circuiting).
5. Gravity flow reagent (excessive reagent injection delay).
6. Incorrect location of reagent control valve (excessive reagent injection delay).
7. Control valve with excessive stick-slip and backlash (limit cycles).
8. Wrong type of electrodes for process conditions (poor 5Rs).
9. Middle signal selection not used (excessive noise and poor 5Rs).
10. Electrodes submersed in a vessel (coating and maintainability problems).
11. Electrodes located in pump suction (bubbles, clumps, and wrenches).
12. Electrodes located too far downstream (excessive measurement delay).

Aaron's Response:

In control system modernization projects – that is, brownfield projects designed to replace and improve the automation systems in plants – the focus is on risk.  Risks come from changes in the control system technology (the literal hardware and software used will be different that what was there before), from the unknowns in existing facilities (often the personnel who implemented the system are no longer around, and documentation is scarce), and in risk to the project itself (running over budget or causing production losses or deferrals).  Because of these risks, manufacturers often reflexively decide to try to reduce or eliminate any changes that they can.  They focus on “replacement in kind” as a method of doing no harm to an existing operation.

For me, this approach is antithetical to the rationale of the project – for what purpose or with what justification would you take on the costs and risks of replacing an automation system with a new one that does exactly what you’ve been doing for the last several decades? This would be the equivalent of replacing your old landline with an iPhone or Android and insisting that it have physical buttons and beeps at you when another call comes in.  While you have kept things the “same,” things are never the same – and you’ve left untold amounts of value on the table along the way.

Over time, we have really mastered an approach to these projects which allows for a true modernization – delivering the newest features and functionality along with state-of-the-art controls – while appropriately mitigating risk. Key to this is proper planning and change management. This is where dynamic simulation comes in. Over the course of these conversations, I hope to highlight a lot of different places and strategies for application of simulation, but here are the main spots:

• Project testing and checkout – simulation enables smoother startup by allowing for testing of scenarios that would otherwise not be testable until after commissioning. This is key to a safe and smooth startup without production impacts.
• Operator training – since operators will have to start up the plant on a new control system, dynamic simulation mitigates risks by getting the operators familiar with the new system and starts to build the muscle memory of running the plant before the stakes are high.
• Performance improvements – these projects are huge opportunities to improve the performance of the plant with better-designed regulatory control, optimized tuning, alarm management, advanced control, state-based control, and improved graphics. Simulation offers the ability to test and validated these new strategies and to deliver real return on the project’s investment while mitigating the risks of change.
  

Ron's Response:

There are a few areas to focus on when developing simulator scenarios.

1. The development of process knowledge, i.e. Distillation, heat exchange, chemical reactions. Scenarios can be created to encourage panel operators to expand on their knowledge of the process. For example, a distillation system is dynamic. Reading about it in a manual and procedures are a good starting point. Seeing how a reboiler issue impacts the rest of the tower and how to minimize the upset develops a new skill level to the panel operators understanding of distillation. 
2. Share experiences from past incidents. This is the best way to ensure that the panel operators understand what happened in past incidents and how to limit the impact if they happen again. Incident reports can be vague on these details. 
3. Response to emergency situations. As mentioned in previous pods it is critical that operations respond to these events correctly and they should be reviewed periodically on the simulator. 
4. Awareness of how a disturbance in one system can impact another system. Most disturbances will affect more than one system. An upset from one system will likely upset the flow etc. to the next system. An operator’s mental model of the process must include the cross impacts of one system to another and scenarios can be developed to practice this. 
5. Develop Situational Awareness. This skill allows the panel operator to be aware of the alarms (light boxes and alarm summary), flaring, impacts to or from other units connected to their area of responsibility, staying connected with their field operators and, be aware if an emergency system is activated (gas detection, safety showers).  

There are many types of failures that can occur. Transmitters and valves can fail many ways. Transmitters can fail high, low, drift either direction, fluctuate, loose the signal. Valves can fail open, closed, last value, cycle, or drift from the requested output. These can all be practiced on a simulator and will build the mental model of the operator. This will increase their chances of detecting a problem and increase their response time.

The timing of scenarios is important. A failure that happens quickly is usually obvious to detect. This will help a new panel operator develop confidence and skills. To challenge an experienced operator a subtle approach is required. Slowly drifting a transmitter will allow the problem to evolve and possibly cause an alarm in another system to come in first. When I first started creating this type of scenario, I thought I may be too devious. We then had a few incidents in the live facility that were more challenging than the ones I developed. 

Scenario development takes preparation, an understanding of the functioning of the simulator, and a thorough knowledge of the process. New scenarios should also be developed periodically to keep the panel operators engaged and challenged. 

Greg's Response:

Production rate can be maximized by a valve position controller (VPC) monitoring coolant valve position. The VPC setpoint is the maximum desirable valve position, and the VPC process variable is the jacket temperature controller output. The use of actual valve position is unnecessary if the coolant valve has a digital positioner. The maximum throttle position setpoint keeps the coolant valve near a point on the installed flow characteristic that has sufficient slope (valve gain) to correct for disturbances. Signal characterization can be used to linearize installed flow characteristic. The output of the VPC for a liquid reactor trims the setpoint of the “leader” reactant flow controller and for a mixed phase reactor trims the setpoint of the liquid and gas reactant flow controller for liquid and gas products, respectively. An enhanced PID with external-reset feedback (dynamic reset limiting) for the VPC eliminates limit cycles from coolant valve backlash, reduces interaction between the VPC and the jacket temperature controller, and enables smoother optimization with faster correction for large disturbances by directional move suppression. Directional move suppression by means of rate limits on the manipulated feed flow setpoints enables a gradual optimization and fast correction for abnormal conditions. 

A reactant feed flow set point rate limit would be fast for correcting an increase in valve coolant position to prevent running out of valve for high heat releases. The setpoint rate limit would be slower for the opposite direction to provide a more gradual optimization. External-reset feedback in the PID automatically prevents integral action from driving the VPC PID output faster than rate limits allow or the feed flow can respond. To see the increase in production rate in fed-batch operation from a higher feed rate, either the batch cycle time must be allowed to decrease or the batch mass to increase. See ISA-TR5.9-2023 PID Algorithms and Performance Technical Report for more details on external-reset feedback.

A dynamic simulation that includes external-reset feedback, all the phases, process time constants, mixing delays, measurement and valve 5Rs, installed flow characteristic, and all thermal time constants is critical for detailing and tuning the best control strategy. 

For much more knowledge, see the ISA book Advances in Reactor Measurement and Control (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

Top Ten Mistakes made in Maximizing Reactor Production Rate

1. Model predictive control (MPC) is used that does not have the aggressive feedback proportional and derivative action needed to prevent a runaway reaction.
2. Real time optimization (RTO) is used that does not account for the positive feedback in exothermic reactions needed to prevent a runaway reaction.
3. Valve position control (VPC) setpoint is too close to coolant valve output limit.
4. Valve position control (VPC) setpoint is on flat part of coolant installed flow characteristic.
5. Quick opening installed flow characteristic from small valve to system pressure drop ratio.
6. Oversized coolant valve causing operation near closed position resulting in on-off control.
7. Tight shutoff coolant valve and tight or graphoil valve packing causing excessive stiction.  
8. Limit cycle from coolant valve backlash and integral action in VPC and valve positioner.
9. Running out of coolant valve from VPC tuning 10 times slower than reactor PID tuning.
10. Not using directional move suppression for smooth gradual optimization with fast getaway.

Ron's Response:

Critical decisions include situations that could include a loss of containment and prompt isolation of the process is required, or when equipment fails and quick response by operations can prevent an outage or loss of production.  There can also be events that require the process to be safe parked when primary equipment fails.

Pattern recognition is an important skill when there is limited time to make a decision. There may not be time to review all the data and all the possible responses. Gary Klein’s Recognition Primed Decision model helps us understand how we make critical decisions. In this model, he explains how we interpret cues from process data to recognize patterns and utilize insights to develop action scripts. A mental simulation is then used to validate the action. This is accomplished from their experiences and their mental models of the process.

Scenario-based training is an effective technique to prepare operators for tough decisions. In this training style, the trainee is given the process data and must detect the problem before they can determine how to correct it. They not only develop pattern recognition skills but also develop critical decision-making skills.

Simulators are an excellent scenario-based training tool. Emergency systems like gas and fire detectors can be included in the model and scenarios developed to train operations to respond to leaks. They can practice initiating the deluge and isolating the process to minimize the release. Flare monitors should also be included in the simulator to highlight the importance of environmental impacts in the response to upsets. If panel operators are trained without flare monitors, they are less likely to consider flaring during an actual process upset in the facility.

Critical thinking is a key skill for panel operators and when used with pattern recognition the impact of process upsets can be minimized. Scenario based training is an effective tool to develop these skills.

Greg's Response:

For gas reactants and a gas product, a pressure loop controls the material balance and provides the time available for reaction at a given production rate by manipulating the discharge product flow to balance the total feed flow. The residence time for these fast reactions is small (e.g., a few seconds) but still must be kept above a low limit. A fluidized catalyst bed is used to promote reaction rate. If a temperature loop manipulates the leader gas reactant flow, the production rate is automatically maximized by the temperature and pressure controllers for a given cooling rate established by boiler feedwater (BFW) flow and the number of coils in service. Direct manipulation of feed rate by the temperature control is possible in gas reactors because the additional time lag for composition response is negligible due to the small residence time and the inverse response at the control points is negligible due to the fast reaction, high heat release, and catalyst heat capacity.

A gas reactor with a fluidized catalyst bed may develop hot spots from localized high reactant concentrations due to a non-uniform flow distribution and no back mixing. Numerous separate cooling coils are used so operations personnel can switch coolant coils in or out of service to deal with hot spots and changes in production rate. However, the switching causes a disturbance to the temperature controller as fast as the BFW on-off valves can move. Numerous thermowells each with multiple sensors traverse the reactor. The average temperature is computed for each traverse with the highest average selected as the control temperature. A feedforward signal can provide preemptive correction for the disruption of coil switching by means of a gain and velocity limit set to match the BFW on-off valve installed characteristic slope and stroking time.

The plug flow of reactants through the reactor provides a tight residence time distribution. 

A dynamic simulation that includes all the phases, process time constants, mixing delays, measurement and valve 5Rs, and all thermal time constants is critical for detailing and tuning the best control strategy. 

For much more knowledge, see the ISA book Advances in Reactor Measurement and Control (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

Top Ten Mistakes made in Fluidized Bed Gas Reactor Temperature Control

1. Use of orifices instead of venturi tubes to provide better reactant flow measurement 5Rs.
2. Use of tight shutoff valves instead of throttling valves to provide better feed valve 5Rs.
3. Poor distribution of feed streams.
4. Poor distribution of catalyst.
5. Coating or plugging in catalyst bed.
6. Hot spots in catalyst bed triggering side reactions.
7. Slow temperature measurement response due to protective tubes or thermowells.
8. Use of thermocouples instead of RTDs to eliminate drift and improve sensor resolution.
9. Not rejecting outlier temperature measurements in computing average bed temperature.
10. Not including enough sensors in cross sections for computing average bed temperature.

Greg's Response:

For both batch and continuous reactors, reaction completion control seeks to provide a complete conversion of all reactants and consequently no excess accumulation of a reactant in a particular phase. If the reactants are in different phases and the product is a single phase, inventory control can be used for reaction completion control. The product must be a gas, liquid, or solids with no recycle streams from downstream or co-products in the other phases.

Using these concepts one can determine whether inventory control provides completion control. For a liquid product, excess gas reactant is inherently prevented by pressure control for both batch and continuous processes. For a gas product, excess liquid reactant is inherently prevented by level control for continuous processes and possibly for solids control via phase separator (e.g., recirculation line hydroclone) for all processes.

For a liquid product, a pressure controller provides continuous completion control by increasing gas feed for a decrease in pressure from a deficiency of gas reactant and by decreasing gas feed for an increase in pressure from an excess of gas reactant. The gas phase reaction is normally fast enough for the gas reactant to be totally consumed in the reaction so that only the inerts are left in the overhead vapor space. An off-gas purge flow prevents the accumulation of inerts. A level controller maintains the liquid material balance by manipulating the liquid product discharge flow.

For a gas product, a level controller provides continuous completion control by increasing liquid feed for a decrease in level for a deficiency of liquid reactant and decreasing liquid feed for an increase in level from an excess of liquid reactant. A purge flow from the bottom prevents the accumulation of inerts in the liquid phase.

The residence time control by the level loop shown for a liquid single-phase reactor could help maintain the best residence time in the gas phase and besides the liquid phase by keeping the bubble rise time constant.

A dynamic simulation that includes all the phases, process time constants, mixing delays, measurement and valve 5Rs, and all thermal time constants is critical for detailing and tuning the best control strategy. 

For much more knowledge, see the ISA book Advances in Reactor Measurement and Control (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

Top Ten Mistakes made in Multiphase Reactor Composition Control

1. Use of impulse lines instead of direct mounting for pressure transmitter.
2. Not minimizing pressure transmitter span to operating pressure range.
3. Not using non contacting radar that would provide exceptionally precise level measurement.
4. Not maximizing pressure controller proportional action.
5. Not minimizing pressure controller reset action.
6. Not maximizing level controller proportional action.
7. Not minimizing level controller reset action.
8. Not sustaining an adequate bottoms purge for gas product.
9. Not sustaining an adequate off-gas purge for liquid product.
10. Not using resident time control previously detailed for liquid single phase reactor.

Ron's Response:

Often times this distinction is not highlighted as each type of procedure presents unique challenges. Yes, there are at least 4 main types of procedures which are common to most operations.

Procedures can be separated into four groups, Startup, Controlled Shutdowns, emergency procedures, and routine duties.

1. Startups – Startup procedures are a challenge to write. They are a combination of events that must happen sequentially (i.e. compressor or convertor startups) and events that happen consecutively (several systems brought online simultaneously). The sequential steps are usually associated with safety logic and must be followed very closely. The consecutive steps are much more fluid and dynamic and may be slightly different for each startup. Therefore, training for this type of procedure involves some memorization and it also requires the development of a solid process mental model that will allow the operators navigate a very dynamic situation. Simulators are the best tool I know of to train operations for both approaches.

    

2. Controlled Shutdowns – These procedures can be straight forward to train for as a series of known steps can be followed to safely isolate and secure the process. The feed can be gradually reduced while production is removed. Flaring can be minimized if strategies are developed, and operations are trained on them. 

    

3. Emergency procedures - These situations can include power failures, instrument air loss, the loss of any equipment that requires the shutdown of the whole process, feed losses, responses to off-specification events or even large rate reductions. Correct responses from operations can minimize the amount of flaring, prevent equipment damage and provide rapid isolation of leaks. Shutdowns can result in sudden temperature and pressure changes. Exceeding the design of exchanger differential temperature limitations can result in head leaks or tube failures. Depressurizing equipment can result in auto-refrigeration in certain processes and possible catastrophic failure of vessels. Training is critical for these events to prevent equipment damage and loss of life. 

    

4. Routine duties – These can include taking equipment out of service for maintenance i.e. pumps, exchangers, control valves, transmitters. Training operations to manage these tasks will prevent process upsets and ensure the equipment is safe for maintenance to work on. The procedure will include the process steps to remove the equipment from service, the hazards of the residual chemicals that may be present and how to safely remove them. Also, the testing required to ensure the equipment has been properly prepared and what isolation is required. 

    

Regardless of the type of procedure, the training will have to include memorization, as well as the development of mental models and tacit knowledge. A procedure will never be able to cover every eventuality. Even for procedures that are very repeatable the operator should understand the reason for every step and understand how every step will impact the process. Without this they may blindly continue even when there is a catastrophe developing. Simulation is an excellent tool to develop and ensure our operators are prepared. 

Ron's Response:

There are benefits and challenges with procedures. Procedures are an essential part of the safe and efficient operation of our process. The best way to highlight these are in a few bullet points. The following is based on research through the Center for Operator Performance with Dr. Gary Klein and Josheph Borders from ShadowBox Training. 

Benefits:

• Our processes are too complex to memorize every step, and not having to think through every step every time reduces the workload. 
• Procedures are great training tools for novices and help to compile experiences or learnings from incidents. 
• Critical tasks require specific sequences of events that if not followed could lead to lost production, hazardous releases, or worse.
• They are a great tool for documenting what steps are required for known emergencies or large process upset situations. The steps required can be discussed and evaluated when there is no time pressure. The more consistently the upsets follow the same pattern, the more successful the procedures will be.
• Procedures can impose consistency and help crews to coordinate across shifts. This is beneficial for activities that take more than one shift and helps the relief crew know where to take over. There are also complex tasks like taking equipment out of service for regeneration or removing fouling that can take coordination of the Panel Operator and the Field Operator. If they have not completed this task together before, then a procedure can ensure they are both approaching it the same way.
• Procedures, practices, and permits are a must for preparing equipment for maintenance. Preparing equipment is a critical task for operations to minimize the risk to maintenance personnel. This takes a coordinated effort between the two groups to ensure the equipment is safe to work on and safely returned to service.

Challenges: 

• They are great in well-ordered situations but become brittle in complex situations that can have many interactions. Every procedure is written with a set of assumptions that usually are not articulated (i.e., steady state, all equipment available and operational, full rates, etc.)
• It is difficult to write a procedure that is in a linear format to capture a multi-variable process where several things could be impacting each other at the same time. A plant start-up is like this. There can be two or more Panel Operators working on different systems that will affect the other systems. A procedure is a good resource for a start-up; however, if you are completely relying on the steps and not interacting with the conditions that present themselves, you will have a challenging start-up.
• It is difficult, if not impossible, to anticipate every possible situation that could happen. A few years ago, a company came and toured my plant’s simulator facility. The visiting company had attempted to write a procedure for every possible problem that could happen. This was not working as well as they had hoped, and they decided to change their approach to improve Operator performance via simulation-based training. Even if you could write a procedure for every possible problem, which I believe would take hundreds or more procedures, how would you find the right one in time to respond?
   

Procedures are crucial for ensuring safe and efficient operations, providing clear guidelines for complex tasks and emergencies, aiding in training, and ensuring consistency across shifts. However, they can be limited by their assumptions and linear format, struggling to adapt to dynamic and multi-variable situations. By using Dynamic Simulation we can balance procedural guidance with the flexibility to adapt to real-time conditions in order to enhance both safety and operational effectiveness.

Greg's Response:

For reactions that are all in one phase (gas, liquid, or solid), inventory control (pressure or level control) cannot not automatically adjust a reactant flow for changes in conversion to prevent an excess or deficiency of reactant in a product phase that is the opposite of the reactant phase. For these reactors, the use of analyzers is more important for maximizing yield beyond what tight temperature control can do.

For well mixed reactors the largest sources of improper reactant concentration leading to excess reactant are errors in reactant flow measurement and changes in reactant composition. Note that a deficiency in one reactant concentration creates an excess of another reactant. Coriolis meters can be used to provide the greatest mass flow measurement precision and rangeability with density correction for any changes in reactant feed concentration. Consequently, Coriolis meters on reactant feeds eliminate most of the sources of reactant unbalances if the mass flow ratios are correct and coordinated to maintain reaction stoichiometry.

Analyzers and inferential measurements can provide composition control to correct the ratio of reactants. If density of the excess reactant is significantly different than the density of the other components in the reactor, a Coriolis meter in the recirculation line can provide an inline inferential measurement of the excess reactant concentration. Inline composition measurements by means of sensors in a vessel or pipeline provide a measurement in a few seconds whereas at-line analyzers with sample systems can have more than 30 minutes of dead time due to sample and analyzer cycle times. Lab or at-line analyzer results must be communicated as quickly as possible to the control system. An Enhanced PID described in Annex E of ISA-TR5.9-2023 Technical Report is used in the composition loop to simplify tuning and prevent cycling from sample and analyzer cycle time. 

A dynamic simulation that includes the positive and negative feedback process time constants, mixing delays, composition measurement 5Rs including transportation delays, and analyzer sample and cycle time is critical for detailing and tuning the best control strategy.  

For much more knowledge, see the ISA book Advances in Reactor Measurement and Control (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

Top Ten Mistakes made in Liquid Single Phase Reactor Composition Control

1. Not achieving tight temperature or reactant mass flow ratio control.
2. Not using Coriolis meter in recirculation line for density and concentration measurement.
3. Not creating an inferential composition measurement from existing in-line measurements.
4. Not sustaining a slight excess concentration of one reactant.
5. Use of analyzer in analyzer house creating a large sample transportation delay.
6. Not using a high sample recirculation flow creating a large sample transportation delay.
7. Lab samples sitting on shelf causing a delay in lab reading and change in sample temperature and possibly composition due to evaporation, precipitation, or reaction. 
8. Not using an Enhanced PID for concentration control using at-line or lab analyzers.
9. Not changing level in proportion to production rate to keep residence time constant.
10. No screening for and rejection of invalid at-line and lab analyzer results.

Ron's Response:

It is easy to be critical during simulator training because of the complexity of our processes and the fact there is so much going on. Remember to acknowledge when something is noticed or dealt with correctly. The intent is to help them develop a thought process. It may seem helpful to point out every mistake, but it is better to help them understand how they arrived at their conclusions and to ask if there may be other information that would be useful. (I must remind myself of this last paragraph frequently). When they are missing something, become curious about it. Explore their understanding and how they may have missed the important information.

Although some pressure is required during training to keep the trainee engaged, the ability to reason declines when stress becomes too high. Memorization is also negatively impacted.

Greg's Response:

Temperature loops control the energy balance and the reaction rate through the Arrhenius equation. A cascade temperature control system offers the greatest linearity and responsiveness to coolant pressure and temperature upsets. The reactor temperature PID manipulates the setpoint of a jacket inlet temperature control that in turn manipulates makeup coolant flow. The coolant exit flow, such as cooling tower water (CTW) return flow, equals the coolant makeup flow to the jacket by piping design and in some case by pressure control in the recirculation system. The resulting constant jacket coolant flow eliminates the increase in dead time, process gain, and fouling from a decrease in jacket flow. The temperature controller PID gain must be maximized for highly exothermic reactors even to the point of causing oscillations in the jacket temperature loop. Highly exothermic reactors can have a runaway response due to positive feedback where too low of a PID gain causes excessive acceleration in temperature response to the point of no return. 

In a liquid reactor a coated sensor or a sensor tip that does not extend past the nozzle into the vessel or a sensor hidden behind a baffle, could cause a measurement time constant larger that is than the thermal time constant. A sensor in a baffle with a glass coating in a small liquid volume will also have an excessive measurement lag due to the poor baffle surface thermal conductivity.

The temperature sensor location is also important for the secondary jacket temperature loop. The sensor should be in the coolant recirculation line rather than in the jacket. The higher velocities and turbulence in the pipeline provide a faster measurement with fewer fluctuations from level and phase changes and cold or hot spots from product sticking on the reactor wall.

A dynamic simulation that includes the positive and negative feedback process time constants, mixing delays, measurement and valve 5Rs, and all thermal time constants from heat transfer surfaces and sensors is critical for detailing and tuning the best control strategy. 

For much more knowledge, see the ISA book Advances in Reactor Measurement and Control (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

Top Ten Mistakes made in Liquid Single Phase Reactor Temperature Control

1. Throttling reactant feeds for temperature control causing inverse response.
2. Throttling jacket flow for temperature control causing poor heat transfer, high secondary loop process gain, and large dead time at low production rate.
3. Not using Coriolis flow meters on reactant feeds causing stoichiometry errors.
4. Use of thermocouples instead of RTDs causing drift and poor accuracy and sensitivity.
5. Sensor not spring loaded and thermowell tip not reaching into well mixed zone of reactor.
6. No lead-lag compensation of ratioed setpoints to provide simultaneous changes preventing momentary stoichiometry errors for changes in production rate that accumulate over time.
7. Reactant feed controllers not tuned for maximum disturbance rejection (e.g., pressure upsets).
8. Direct addition of steam into jacket causing bubbles and droplets in jacket heater from transitions between heating and cooling instead using steam injection heater.
9. Not maximizing PID gain and rate action and minimizing reset action in reactor temperature controller (most reactor temperature PID reset times are one to two orders of magnitude too small).
10. Not narrowing jacket temperature controller scale range to operating range causing a loss in jacket temperature loop performance.

Greg's Response:

Lack of recognition of the adverse effects of changes in process stream composition and operating conditions, upstream and downstream piping, and velocity profile in differential pressure (d/p) measurements and vortex meters being mistakenly pervasively used. The extensive problems with impulse line fill and length are additional problems for d/p measurements. Dynamic simulations that include the effect of installation on 5Rs noted last week and first principle relationships to show the effect of stream composition and operating conditions on flow measurement can lead you to the best solution and avoid the following common mistakes:   

Top Ten Mistakes in Flow Measurement Specification

Lack of recognition of adverse effect on accuracy and rangeability of

1. Density changes
2. Viscosity changes
3. Low flows
4. Large meter size
5. Large flow span
6. Low Reynolds Number
7. Erratic nonuniform velocity profile
8. Insufficient upstream piping straight run
9. Insufficient downstream piping straight run
10. Accuracy in % span instead of % reading

All items apply to differential pressure (DP) flow measurements and vortex meters.  DP flow measurements have the significant additional problem of impulse lines and capillaries detailed in the Control Talk columns “Prevent pressure transmitter problems” and “Your DP problems …”. A vortex meter rangeability is less than expected because a line size meter often has a maximum velocity that is much greater than the velocity associated with the vortex meter span max flow. 

The rangeability and accuracy of magnetic flowmeters and Coriolis flowmeters is typically 5 and 25 times better, respectively than DP and vortex flowmeters. Plus, their accuracy is in % reading instead of % span, greatly helping accuracy at low flows.  For more knowledge, see the Control Talk column “Knowing the best is the best” and the ISA book Essentials of Modern Measurements and Final Elements in the Process Industry (use promo code ISAGM10 for a 10% discount on Greg’s ISA books).

Ron's Response:

Depending on the complexity of your process it can be impossible to write a procedure of every upset. If this was accomplished, could you find the right one in time. Another approach is to train the panel operators to gather information and think through problems. 

Going through situations that are not proceduralized develop information gathering and problem-solving skills. Start with basic malfunctions and evolve to the more complex. Even beginning with determining the difference between a valve failing closed compared to the failure of a flow transmitter is beneficial. They may initially look the same from the graphics unless you have feedback from the valve to the control room. 

Ask them to verify their initial assumptions. Are there indications upstream or downstream of the problem that can validate theories? As the simulator trainer, you will also be acting as the Field Operator and must respond to their requests for a field check. I typically deliver the answers from a recently qualified Operator's perspective and require that I be asked to check everything and not volunteer any information. 

The expectation is that these are growing experiences, and they may not be successful on all of them initially. It is important to distinguish between when they are training versus when they are being tested. If they know it is a training exercise, they will ask more questions and be more open about their thought process. Be clear on what the expectations are. 

They should be able to start the process and manage all the emergency procedures, including shutting the process down. Also, they can handle normal malfunctions, although I like to include some challenging scenarios that are intended to get them to think a little deeper where they may not be successful initially. 

I used to wonder if I was being too devious until I realized the real process sometimes delivered some very challenging problems to our Operators. The sign of a challenging scenario is when it will cause the first alarm to come in at a different system than the system with the problem. 

Also, include at least one process leak scenario that requires them to isolate a part of the process and requires them shut down the plant. There is typically a lot of hesitation to do this. Most of the training is focused on keeping the process online.  Having to make this decision at least once in training will help the trainee work through this if a large leak ever happens. 

Training for upsets on a simulator develops a problem-solving mindset that can be applied to many different failures that have similarities.

Greg's Response:

Process efficiency and capacity are often determined by a temperature control loop performance’s effect on the formation and purification of the product. Good composition control in biological and chemical reactors and in distillation columns is achieved by tight temperature control.

There is a significant misunderstanding as to the best selection, specification, and installation of temperature measurements aggravated by the lack of inclusion of the 5Rs (resolution, repeatability, rangeability, response time, and reliability), drift, and nonlinearity in measurement specifications. The inclusion of the 5Rs in dynamic simulations can help motivate the use of the best temperature measurements. Dynamic simulations should include several time constants that are the thermal lags associated with the thermowell, modeling objects to simulate the sensor resolution and repeatability, a steadily increasing error to simulate sensor drift, and a constant signal to simulate sensor failure. The detailed following list of Top Ten Mistakes alerts us to the significance and extent of the problem besides directing us to the best temperature measurement.  

Top Ten Mistakes in Temperature Measurement Specification

1. Thermocouple (TC) instead of Resistance Temperature Detector (RTD) for < 1600 oF.
2. Direct wiring of sensor to TC or RTD I/O cards.
3. Loose fit of sensor in thermowell.
4. Sensor not touching bottom of thermowell.
5. Focus on TC versus RTD sensor instead of thermowell response time.
6. Thermowell length and installation results in sensor seeing jacket temperature.
7. Thermowell length and installation results in low velocity at tip.
8. Transmitter span too large.
9. Transmitter remote mounted.
10. Thermowell wall at tip too large

The best temperature measurement uses a head mounted narrow span RTD transmitter on a stepped thermowell with a tight fit spring-loaded sheathed platinum resistance temperature detector (PRTD) mounted in a piping elbow to sure sufficient length and velocity (e.g., liquids > 5 fps).

The ISA book Advanced Temperature Measurement and Control Second Edition details how to get the best temperature measurement and control. Here is Table 2.8 from the book:

Ron's Response:

Freeze up is an unfortunate response to becoming overwhelmed. Reading through a procedure is a different experience than a major event or plant shutdown when the alarm page is flooded, and emergency alarms are blaring. There can also be radio calls, phone calls, communication with other panel operators or outside operators.

Running through the emergency procedures is the next knowledge progression after startup training. These are events like power failures, instrument air failures, or large compressor trips. Anything that has a large impact on the process and the results are quite predictable.

There can be a hesitancy to shut down the process or make large process changes to manage a major upset. For events like these it is helpful to review what the key indicators are that a certain set of actions (emergency procedure) are required. For example, large condensing steam turbines will have to be tripped if the cooling water pumps fail. Review which process variables need be checked to make that decision and what graphic they are on.

Understanding the reasons for each step and chunking up key steps can be helpful. There are likely similar steps in several of the procedures. Thought should be given to what should be memorized and which steps in a procedure can be used as a reference. Generally, the first five to ten minutes in a major process upset require immediate response and should be memorized. This will depend on your process.

The proper execution of emergency procedures is critical and should not be left to chance.

A simulator is a very powerful tool and can be used for a variety of purposes. Improving Emergency Procedures is just one of them. A simulator training program consists of preparatory work and hands-on experience, where board operators practice key routines such as startup, emergency procedures, and handling malfunctions or failures. These will be covered in future ProseraPods.

Ron's Response:

Process startups can be very challenging as there can be several systems coming online at the same time. This can be very challenging to cover in a step-by-step procedure when several activities can overlap on different pages of the procedure. Simulator training allows the operator to develop a mental model of the timing and interactions.

I believe starting up the equipment first is the most beneficial. It allows the trainee to work through all the controllers, and associated logic. It allows them to build some confidence. Hitting them with malfunctions right from the start can be overwhelming.

Having them review the start-up procedures with a qualified Operator before the training is helpful and then again just before going through them on the simulator. Highlighting the key steps and explaining the intent of each step can make this easier to manage. 

Understanding the reasons for each step and being able to think it through is preferred to only following each step of the procedure. This will prepare them to think through problems as there typically is some sort of failure during a start-up.

A simulator is also an excellent tool to improve startups which reduce flaring losses and allow the unit to reach full capacity faster. Different approaches can be tested and validated before being implemented in the unit. The procedures can be updated and then as importantly operations can be trained and allowed time to buy into the new approaches.

A simulator is a very powerful tool and can be used for a variety of purposes. Improving Process startups is just one of them. A simulator training program consists of preparatory work and hands-on experience, where board operators practice key routines such as startup, emergency procedures, and handling malfunctions or failures. These will be covered in future ProseraPods.

Greg's Response:

In my 50+ year career in process automation, dynamic first principle simulations have played a more extensive and critical role in pH system design than any other process application, I was fortunate enough to home in on the charge balance started by Greg Shinskey’s book pH and pION Control in Process and Waste Streams for my Master’s Thesis in Process Control.  I found the charge balance could be readily setup for complex solutions and simply expanded to handle acids and bases with two or more dissociations, different solvents, salts, and ionic strength by the inclusion of multiple dissociation constants and activity coefficients. The books I had then and even now on ionic equilibrium focus on directly solving equations requiring a focus on simple aqueous solutions (e.g., single acid and single base water streams). I found that my much more general and extensive charge balance could provide a result within pH electrode accuracy in 8 iterations of a robust and simple interval halving search. 

Another major discovery on my part not mentioned in the literature is the need to add a small amount of carbonic acid from simple exposure to the carbon dioxide in air to match the lab titration curve. The simple addition of carbonic acid can reduce the change in process gain by orders of magnitude in the neutral region for a strong acid and strong base system. Besides an accurate titration curve, the inclusion in the model of reagent transportation delays in piping and dip tubes, mixing nonuniformity in pipes and vessels, valve stiction and backlash, and the 5Rs of electrode response (resolution, repeatability, rangeability, reliability, and response time), is critical. 

The Digital Twin simulation using a charge balance with carbon dioxide added to match the lab titration curve can be used to improve every aspect of pH system design justifying expenditures on better mixing, piping, control valves, and electrodes, as detailed in my 2024 ISA book Advanced pH Measurement and Control Fourth Edition. The capital savings from reducing the number of vessels required by better system design can be hundreds of thousands of dollars. 

A Digital Twin model can also update the titration curves and adapt PID controller tuning settings and signal characterization used to convert the controlled variable from pH to linear reagent demand. Just taking the time to read the best practices at the end of each chapter, will enormously help you get on the right path to the right solution.

Greg's Response:

The biggest problem facing nearly all control loops stems from control valve specifications not requiring the control valve internal closure member to actually move and the flow to reasonably change for a change in valve signal. The lack of specification entries for precision, response time, and installed flow characteristic is baffling. The entries for capacity and leakage and emphasis on reducing pressure drop and cost, has led to valves with excessive stroking time, stiction, lost motion, shaft windup, and nonlinearity. The problem is accentuated by the term “high performance” valves that have higher capacity, tighter shutoff, lower pressure drops, and lower cost but are actually “on-off” valves posing as “throttling” valves. Even the best positioner cannot overcome the inherent detrimental results in terms of poor control. Often the positioner is being lied to because the feedback mechanism is moving in response to changes in actuator signal but the internal closure member is not moving due to stiction, lost motion, and shaft windup.

I have made it my goal for the last 40 years to turn this around. I have developed models that simulate the stiction and lost motion, pre-stroke deadtime, stroking time, time constants, and installed valve characteristic for control valves. I have published many articles most notably “How to specify valves and positioners that do not compromise control”. I have also written the ISA-TR75.25.02 Annex A - Valve Response and Control Loop Performance - Sources, Consequences, Fixes, and Specifications and ISA-TR5.9-2023 Annex C Valve positioners.  All process control applications with control valves should use these models and the Annexes I have written for ISA Technical Reports.

The best control valves for throttling are single plug, “flow-to-open” globe valves with high performance Teflon packing, valve to system pressure drop ratio greater than 0.25, oversized diaphragm actuators, and digital positioners with high gain setting and no integral action, and if necessary to reduce stroking time a volume booster on positioner output with bypass valve slightly open. If a rotary valve must be used, it should use direct splined shaft connections and not have any seal friction. Not realized is that integral action in the positioner reduces the allowable gain used in the positioner and increases the amplitude and period of oscillations from stiction and lost motion. To further drive home the critical importance of using dynamic models of valve response to ascertain and justify the best control valve here are the Top 10 Mistakes in Control Valve Specification:

1. Excessive flow capacity decreasing rangeability and increasing the oscillations from stiction and lost motion.
2. Low valve to system pressure drop ratio increasing nonlinearity, decreasing rangeability, and increasing the oscillations from stiction and lost motion.
3. Low leakage decreasing rangeability and increasing the oscillations from stiction and lost motion.
4. Keylock connection of actuator to rotary valve shaft increasing lost motion. 
5. Link-arm connection of actuator to rotary valve shaft increasing lost motion.
6. Rack and Pinion connection of actuator to rotary valve shaft increasing lost motion.
7. Scotch-Yoke connection of actuator to rotary valve shaft increasing lost motion.
8. Graphite packing increasing stiction.
9. Booster instead of positioner causing unstable diaphragm actuator.
10. Integral action and low gain setting in positioner.
    
    

Ron's Response:

Although there may be many ways to approach simulator training, I will discuss the approach I use and why. This approach may have to be adapted depending on the schedules and availability of the operators to train. Because of this, some preparation is recommended to make the best use of the simulator training time.

The first step is to have the operators read the manuals and procedures, as mentioned in the first ProseraPod. They can then review the graphics at the actual console with a qualified panel operator to become familiar with navigating the graphics and understanding the basic control loops. This can then be followed up with how to complete a “Round” on the panel and check all the variables to ensure they are within normal parameters. This can be completed on the simulator as well if there is availability. This is a good start to be able to benefit from simulator training and to be able to absorb the first lessons.

A simulator training program consists of preparatory work and hands-on experience, where board operators practice key routines such as startup, emergency procedures, and handling malfunctions or failures. These will be covered in future ProseraPods.

Greg's Response:

Abnormal operating conditions not only pose process safety and performance issues but also potentially cause equipment damage and environmental violations. Often operator actions are not timely and not sufficient, possibly even wrong making the problem worse. State-based control developed and tested using a Digital Twin with dynamic first principle models can find and implement the best solution and provide training of operators, engineers, and technicians enabling continuous improvement. 

Classic cases are state-based control to prevent compressor surge and Resource Conservation and Recovery Act (RCRA) pH violations. Compressor flow can completely reverse direction in a few hundredths of a second and cause fast (<1 sec period) nearly full scale forward and reverse flow oscillations. PID controllers can not deal with these oscillations and will not be able to stop the surge cycles. Fortunately, the pressure versus suction flow characteristic curve to the left of the surge curve including negative flow normally not seen in the literature or provided by the compressor manufacturer, can be modeled based on equations and figures in my free book Centrifugal and Axial Compressor Control and implemented in a Digital Twin dynamic simulation. Compressor surge can potentially damage rotors in axial compressors and seals in all compressors and cause downstream shutdowns. Future-value blocks can predict a surge event before the operating point crosses the surge curve enabling state-based control to put the PID surge controller in remote output or output tracking (e.g., open-loop backup) with an output large enough to prevent surge. The optimum point of return to closed loop control can also be predicted to bumplessly put the PID surge controller back in the automatic mode. 

Similarly, the Digital Twin simulation using a charge balance with carbon dioxide added to match the lab titration curve can use state-based control and a future-value block to predict a possible RCRA pH violation and trigger an open-loop backup and bumpless return to automatic mode of pH PID effectively addressing the pH disturbance as detailed in my 2024 ISA book Advanced pH Measurement and Control Fourth Edition. The Digital Twin can also update the surge curve and titration curves based on observed changes in the controlled and manipulated variables.

Ron's Response:

Most programs to train and qualify panel operators start the same way. The trainee will read all the associated manuals which are usually followed by some written or electronic test questions. These questions can also be about the associated procedures, or the procedures are reviewed with a qualified operator. All very good strategies to get to know the process.

Even with all this training, I believe most panel operators would say they struggled when they had to handle their first process upset and that they did not feel prepared to make the required decisions. The analogy I like to use is if we trained a Formula 1 driver on the freeway. They would get some great experience traveling at 70 MPH and although the experience can seem scary to some, it does not compare to a Formula 1 race. They can be traveling at speeds over 200 MPH and then must prepare for a hairpin corner. Could you imagine how poorly they would perform if the first time they drove on a Formula 1 racetrack was on race day? This is what we are asking of our panel operators if we do not allow them to practice upset responses prior to an event in the actual process. Except I believe our processes are more complex than a Formula 1 race. This is why we should have a simulator training program.

A simulator training program consists of preparatory work and hands-on experience, where board operators practice key routines such as startup, emergency procedures, and handling malfunctions or failures. These will be covered in future ProseraPods.

Greg's Response:

Startups and product or raw material mix transitions performance is particularly nonrepeatable because of manual actions, operator skill limitations and variations, complex dynamics due to a nonequilibrium, and large dead times from low flow rates. Consequently, startups and transitions are vulnerable to Safety Instrumented System activation and excessive losses in process efficiency and capacity. 

Digital Twin dynamic first principle models along with operator training sessions and interviews can find the best operator actions. Implementation of these actions per ANSI/ISA-106.00.01-2023 “Procedure Automation for Continuous Processes” Standard can be continuously improved by prototyping and testing in the Digital Twin leading to much faster, safer, and more productive startups and transitions. The automation often simply consists of putting key PID controllers in remote output or output tracking modes and setting and holding optimum PID outputs making a bumpless transition to automatic control at the best point in the startup or transition. Level and pressure controls are generally commissioned early in the startup or transition to help enforce material balances. When flows are greater than the low flow rangeability limit of flow measurements, flow ratio control is used. Once process and stream conditions are stabilized, composition, pH, and temperature controllers are commissioned to correct flow ratios. 

The Digital Twin can help find and test the best flow controller location in recycle stream path to prevent an unstable process response due the positive feedback of recycle stream composition changes. The Digital Twin can also help adapt the procedure automation to deal with changes in stream compositions and PID tuning requirements.  

Greg's Response:

Dynamic first principle simulations with instrumentation dynamics included can help find, test, and tune the inner loop for cascade control so that it can correct for disturbances before they significantly affect the outer loop. The outer closed loop time constant needs to be 5 times larger than the inner closed loop time constant to reduce oscillations from interactions between the loops. This is best achieved by fast process and instrumentation dynamics in the inner loop. 

Often unrecognized are the rangeability problems of the inner loop measurement especially for differential head and vortex flow meters. 

• Online dynamic simulations can bumplessly substitute an inferential measurement based on installed valve characteristic and stream operating conditions when the rangeability is exceeded. 

• Online dynamic simulations can also adapt PID tuning so that the outer closed loop time constant stays 5 times larger than the inner closed loop time constant for increases in process and sensor delays and lags for low production rates and fouling. 

A dynamic simulation in a Digital Twin can test the setup and show the value of filtered positive feedback integral action to suppress oscillations. Chapter 11 in my Tuning and Control Loop Performance Fourth Edition (free to download) has the recommendations, test results, and key points for cascade control.

Greg's Response:

Override control is considerably challenging because the controllers that are not selected tend to windup, the takeover of control is difficult to make bumpless, controller tuning depends upon dynamics that may be quite different for the situation when override occurs, and operator confusion as to what is happening is significant, leading to detrimental intervention. 

The good news is that PID algorithms with filtered positive feedback can make the transition smoother and dynamic first principle simulations can adapt the PID tuning settings to deal with changing process conditions, develop metrics to show time each override control has taken over and consequential process performance for last hour and shift, and provide the testing and training to ensure better understanding and continuous improvement of override control. 

For a deep dive into details and test results, see the Control magazine feature article “The pitfalls and promise of override strategies” that I coauthored with Peter Morgan. For much more on filtered positive feedback see the ISA Technical Report “Proportional-Integral-Derivative (PID) Algorithms and Performance” ISA-TR5.9-2023 that Peter and I led and were recognized for by ISA Excellence in Standards awards.

Greg's Response:

Ratio control is much more effective than flow feedforward control if there are good flow measurements. Ratio control enables the operator to see and if necessary, adjust a flow ratio. Many unit operations startup on ratio control without process control feedback until the process reaches equilibrium conditions. It is particularly important that extensive ratio control (e.g., distillate to feed, steam to feed, and bottoms to feed ratios) be used in the startup of distillation columns until the temperatures and concentrations reach normal operating conditions. Dynamic simulations are used in the same way as was done for feedforward control to provide the dynamic compensation needed. Ratio and bias-gain blocks are used in the PID configuration where the operator can see the actual ratio and manipulate a desired ratio to handle startup and abnormal operating conditions. Dynamic Simulation is critical to provide the guidance for the operators needed in startup and for equipment and instrumentation problems. Dynamic simulation can be used to automate the startup by procedure automation or automate solutions by state-based control.

When the process is ready for PID control, the process PID manipulates the ratio block setpoint (equivalent to a feedforward multiplier used in dead time dominant processes) with an adaptive PID manipulating the bias/gain block bias or the process PID manipulates the bias/gain block bias (equivalent to the more prevalent feedforward summer described in last week’s post) with an adaptive PID manipulating the ratio block setpoint. Simulation can find how the dynamics change with operating conditions and the adaptive PID tuning to provide a gradual approach to the goal of negligible feedback correction of feedforward by the process PID with minimal interaction between the process and adaptive PID controllers.

Greg's Response:

There are many measured and unmeasured disturbances to process inputs (load disturbances). A feedforward correction needs to arrive at the same point in the process at the same time as the load disturbance with an effect that is equal to and opposite of the load disturbance. Dynamic simulation is essential to finding load disturbances and identifying feedforwards, and the dynamic compensation to provide the corrections with the right timing and size. The compensation changes with operating conditions and may need to be suppressed if unmeasured disturbances are driving the controlled variable back to setpoint. If the feedforward arrives too soon, inverse response can occur. If the feedforward correction is too large, a disturbance in the opposite direction is created. These situations cause oscillations that are confusing to the process PID controller and operations. 

Dynamic compensation of the feedforward signal by means of a lead-lag block and a gain are used to provide the correction with the right timing and size. The feedforward lag is set equal to the load lag (disturbance variable path lag), the feedforward lead is set equal to the loop lag (controller output path lag). The feedforward gain is the loop gain divided by the load gain and is generally set slightly lower to prevent creating a disturbance in the opposite direction due to nonlinearities and unknowns. Dynamic compensation can be adapted based on how loop and load dynamics change with operating conditions. Intelligence can be added that detects how much an unmeasured disturbance is causing the controlled variable to move in the same direction as the feedforward correction requiring suppression of the feedforward correction. 

Dynamic simulation with a Future-Value block can predict how much an unmeasured disturbance will drive the controlled variable back to setpoint. The feedforward gain could then be reduced by the ratio of the unmeasured load predicted error to the measured load predicted error. An adaptive PID controller can be setup to adjust the feedforward gain to minimize the feedback correction of the feedforward done by the process controller. Simulation can find the adaptive PID tuning to provide a gradual approach to zero feedback correction of feedforward by the process PID that minimizes interaction between the process and adaptive PID controllers.

Greg's Response:

Essentially all processes are nonlinear where the open loop gain, time constants, and dead times change with operating conditions. These changes are generally quite large for changes in production rates and deterioration in unit operations (e.g., catalyst activity, fouling, plugging, …). First principle dynamic models can identify the consequential changes in process dynamics. This knowledge can be used in adaptive PID tuning. For production rate, the update may be simply based on feed rate. For degradation in unit operations, changes in loop dynamics identified in the models can be used to update the PID tuning settings. The knowledge needed can be rapidly gained by running dynamic models much faster than real time (e.g., 100x real time). The results can be tested in a Digital Twin with the actual control system that is running somewhat faster than real time (e.g., 10x real time). There also the possibility of a dynamic simulation running in sync with the PID to update the tuning settings more continuously. First principles dynamic models can be used to implement adaptive PID Tuning and improve process operating conditions.